Рациональное и иррациональное число: описание и чем они отличаются?
Понятие о вещественных (действительных) числах, рациональные и иррациональные числа
Содержание
 Рациональные и иррациональные числа. Понятие о вещественных числах Рациональные и иррациональные числа. Понятие о вещественных числах |
 Иррациональность числа Иррациональность числа 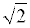 |
 Десятичные приближения иррациональных чисел с недостатком и с избытком Десятичные приближения иррациональных чисел с недостатком и с избытком |

Рациональные и иррациональные числа. Понятие о вещественных числах
Целые числа и рациональные дроби (простые дроби и смешанные числа) составляют множество рациональных чисел, которое принято обозначать буквой Q .
Каждое из рациональных чисел можно представить в виде
 ,
,
где m – целое число, а n – натуральное число.
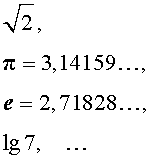
и т.п. являются примерами иррациональных чисел.
Иррациональные числа нельзя представить в виде дроби, числитель которой является целым числом, а знаменатель натуральным числом.
При обращении иррациональных чисел в десятичные дроби получаются бесконечные непериодические десятичные дроби. Множество иррациональных чисел бесконечно.
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Множество вещественных чисел обозначают буквой R .
Иррациональность числа 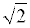
Проведем доказательство иррациональности числа 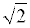 методом «от противного». С этой целью предположим, что число
методом «от противного». С этой целью предположим, что число 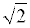 является рациональным числом. Тогда существует дробь вида
является рациональным числом. Тогда существует дробь вида
 ,
,
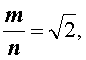
и такая, у которой числитель и знаменатель являются натуральными числами, не имеющими простых общих делителей.
Используя данное равенство, получаем:
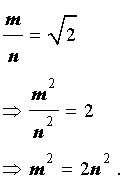
Отсюда вытекает, что число m 2 является четным числом, а, значит, и число m является четным числом. Действительно, если мы предположим противное, т.е. предположим, что число m является нечетным числом, то найдется такое целое число k , которое удовлетворяет соотношению
т.е. m является нечетным числом. Полученное противоречие доказывает, что число m является четным числом. Значит, найдется такое целое число k , которое удовлетворяет соотношению
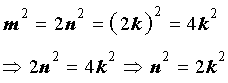
Отсюда вытекает, что число n 2 является четным, а, значит, и число n является четным числом.
Итак, число m является четным, и число n является четным, значит, число 2 является общим делителем числителя и знаменателя дроби
 .
.
Полученное противоречие доказывает, что несократимой дроби, удовлетворяющей соотношению
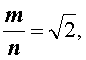
не существует. Следовательно, число 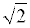 является иррациональным числом, что и требовалось доказать.
является иррациональным числом, что и требовалось доказать.
Десятичные приближения иррациональных чисел с недостатком и с избытком
Разберем понятие десятичных приближений иррациональных чисел с недостатком и с избытком на конкретном примере. Для этого рассмотрим иррациональное число
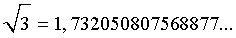
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью.
Последовательностью десятичных приближений числа 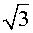 с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа
с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа 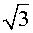 отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.
отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего десятичного знака и т.д.
Если последний десятичный знак каждого десятичного приближения числа с недостатком увеличить на 1 , то получится десятичное приближение числа с избытком.
Само число 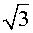 располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.
располагается между каждым своим приближением с недостатком и соответствующим ему приближением с избытком.
Для числа 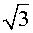 возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:
возникающая бесконечная последовательность десятичных приближений с недостатком и с избытком, имеет следующий вид:
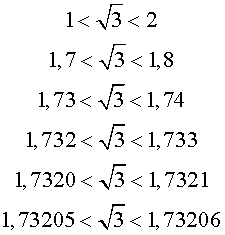
Точно также можно построить последовательность десятичных приближений с недостатком и с избытком для любого иррационального числа.
math4school.ru



- НОВОСТИ
- ПОЛЕЗНЫЕ САЙТЫ
- КАРТА САЙТА
- КНОПКИ САЙТА
- ГРУППА VK
- КОНТАКТЫ






Рациональные и иррациональные числа

Немного теории
Рациональное число – число, представляемое обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Любое рациональное число представимо в виде периодической бесконечной десятичной дроби. Множество рациональных чисел обозначается Q.
Если действительное число не является рациональным, то оно иррациональное число. Десятичные дроби, выражающие иррациональные числа бесконечны и не периодичны. Множество иррациональных чисел обычно обозначается заглавной латинской буквой I.
Действительное число называется алгебраическим, если оно является корнем некоторого многочлена (ненулевой степени) с рациональными коэффициентами. Любое неалгебраическое число называется трансцендентным.
Множество рациональных чисел располагается на числовой оси всюду плотно: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел Q и множество натуральных чисел N эквивалентны, то есть между ними можно установить взаимно однозначное соответствие (все элементы множества рациональных чисел можно перенумеровать).
Множество Q рациональных чисел является замкнутым относительно сложения, вычитания, умножения и деления, то есть сумма, разность, произведение и частное двух рациональных чисел также являются рациональными числами.
Все рациональные числа являются алгебраическими (обратное утверждение – неверное).
Каждое вещественное трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число (а значит, и бесконечное множество иррациональных чисел).
Множество иррациональных чисел несчётно.
При решении задач бывает удобно вместе с иррациональным числом a + b √ c (где a, b – рациональные числа, с – целое, не являющееся квадратом натурального числа) рассмотреть «сопряжённое» с ним число a – b √ c : его сумма и произведение с исходным – рациональные числа. Так что a + b √ c и a – b √ c являются корнями квадратного уравнения с целыми коэффициентами.
Задачи с решениями
в) число √ 2 + 3 √ 3 ;
а) Допустим, что число √ 7 рациональное. Тогда, существуют такие взаимно простые p и q, что √ 7 = p/q, откуда получаем p 2 = 7q 2 . Так как p и q взаимно простые, то p 2 , а значит и p делится на 7. Тогда р = 7k, где k – некоторое натуральное число. Отсюда q 2 = 7k 2 = pk, что противоречит тому, что p и q взаимно просты.
Итак, предположение ложно, значит, число √ 7 иррациональное.
б) Допустим, что число lg 80 рациональное. Тогда существуют такие натуральные p и q, что lg 80 = p/q, или 10 p = 80 q , откуда получаем 2 p–4q = 5 q–p . Учитывая, что числа 2 и 5 взаимно простые, получаем, что последнее равенство возможно только при p–4q = 0 и q–p = 0. Откуда p = q = 0, что невозможно, так как p и q выбраны натуральными.
Итак, предположение ложно, значит, число lg 80 иррациональное.
в) Обозначим данное число через х.
Тогда (х – √ 2 ) 3 = 3, или х 3 + 6х – 3 = √ 2· (3х 2 + 2). После возведения этого уравнения в квадрат получаем, что х должен удовлетворять уравнению
х 6 – 6х 4 – 6х 3 + 12х 2 – 36х + 1 = 0.
Его рациональными корнями могут быть только числа 1 и –1. Проверка же показывает, что 1 и –1 не являются корнями.
Итак, данное число √ 2 + 3 √ 3 является иррациональным.
2. Известно, что числа a, b, √ a – √ b , – рациональные. Докажите, что √ a и √ b – тоже рациональные числа.
( √ a – √ b )·( √ a + √ b ) = a – b.
Число √ a + √ b , которое равно отношению чисел a – b и √ a – √ b , является рациональным, так как частное от деления двух рациональных чисел – число рациональное. Сумма двух рациональных чисел
½ ( √ a + √ b ) + ½ ( √ a – √ b ) = √ a
– число рациональное, их разность,
½ ( √ a + √ b ) – ½ ( √ a – √ b ) = √ b ,
тоже рациональное число, что и требовалось доказать.
3. Докажите, что существуют положительные иррациональные числа a и b, для которых число a b является натуральным.

4. Существуют ли рациональные числа a, b, c, d, удовлетворяющие равенству
(a + b √ 2 ) 2n + (c + d √ 2 ) 2n = 5 + 4 √ 2 ,
где n – натуральное число?
Если выполнено равенство, данное в условии, а числа a, b, c, d – рациональные, то выполнено и равенство:
(a – b √ 2 ) 2n + (c – d √ 2 ) 2n = 5 – 4 √ 2 .
Но 5 – 4 √ 2 (a – b √ 2 ) 2n + (c – d √ 2 ) 2n > 0. Полученное противоречие доказывает то, что исходное равенство невозможно.
Ответ: не существуют.
5. Если отрезки с длинами a, b, c образуют треугольник, то для всех n = 2, 3, 4, . . . отрезки с длинами n √ a , n √ b , n √ c так же образуют треугольник. Докажите это.
Если отрезки с длинами a, b, c образуют треугольник, то неравенство треугольника даёт
Поэтому мы имеем
( n √ a + n √ b ) n > a + b > c = ( n √ c ) n ,
n √ a + n √ b > n √ c .
Остальные случаи проверки неравенства треугольника рассматриваются аналогично, откуда и следует заключение.
6. Докажите, что бесконечная десятичная дробь 0,1234567891011121314. (после запятой подряд выписаны все натуральные числа по порядку) представляет собой иррациональное число.
Как известно, рациональные числа выражаются десятичными дробями, которые имеют период начиная с некоторого знака. Поэтому достаточно доказать, что данная дробь не является периодической ни с какого знака. Предположим, что это не так, и некоторая последовательность T, состоящая из n цифр, является периодом дроби, начиная с m-го знака после запятой. Ясно, что среди цифр после m-го знака встречаются ненулевые, поэтому в последовательности цифр T есть ненулевая цифра. Это означает, что начиная с m-ой цифры после запятой, среди любых n цифр подряд есть ненулевая цифра. Однако в десятичной записи данной дроби должна присутствовать десятичная запись числа 100. 0 = 10 k , где k > m и k > n. Понятно, что эта запись встретится правее m-ой цифры и содержит более n нулей подряд. Тем самым, получаем противоречие, завершающее доказательство.
7. Дана бесконечная десятичная дробь 0,a1a2. . Докажите, что цифры в ее десятичной записи можно переставить так, чтобы полученная дробь выражала рациональное число.
Напомним, что дробь выражает рациональное число в том и только том случае, когда она периодическая, начиная с некоторого знака. Цифры от 0 до 9 разделим на два класса: в первый класс включим те цифры, которые встречаются в исходной дроби конечное число раз, во второй класс – те, которые встречаются в исходной дроби бесконечное число раз. Начнем выписывать периодическую дробь, которая может быть получена из исходной перестановкой цифр. Вначале после нуля и запятой напишем в произвольном порядке все цифры из первого класса — каждую столько раз, сколько она встречается в записи исходной дроби. Записанные цифры первого класса будут предшествовать периоду в дробной части десятичной дроби. Далее, запишем в некотором порядке по одному разу цифры из второго класса. Эту комбинацию объявим периодом и будем повторять ее бесконечное число раз. Таким образом, мы выписали искомую периодическую дробь, выражающую некоторое рациональное число.
8. Доказать, что в каждой бесконечной десятичной дроби существует последовательность десятичных знаков произвольной длины, которая в разложении дроби встречается бесконечно много раз.
Пусть m – произвольно заданное натуральное число. Разобьем данную бесконечную десятичную дробь на отрезки, по m цифр в каждом. Таких отрезков будет бесконечно много. С другой стороны, различных систем, состоящих из m цифр, существует только 10 m , т. е. конечное число. Следовательно, хотя бы одна из этих систем должна повторяться здесь бесконечно много раз.
Замечание. Для иррациональных чисел √ 2 , π или е мы даже не знаем, какая цифра повторяется бесконечно много раз в представляющих их бесконечных десятичных дробях, хотя каждое из этих чисел, как легко можно доказать, содержит по крайней мере две различные такие цифры.
9. Докажите элементарным путём, что положительный корень уравнения
Для х > 0 левая часть уравнения возрастает с возрастанием х, и легко заметить, что при х = 1,5 она меньше 10, а при х = 1,6 – больше 10. Поэтому единственный положительный корень уравнения лежит внутри интервала (1,5; 1,6).
Запишем корень как несократимую дробь p/q, где p и q – некоторые взаимно простые натуральные числа. Тогда при х = p/q уравнение примет следующий вид:
p 5 + pq 4 = 10q 5 ,
откуда следует, что р – делитель 10, следовательно, р равно одному из чисел 1, 2, 5, 10. Однако выписывая дроби с числителями 1, 2, 5, 10, сразу же замечаем, что ни одна из них не попадает внутрь интервала (1,5; 1,6).
Итак, положительный корень исходного уравнения не может быть представлен в виде обыкновенной дроби, а значит является иррациональным числом.
10. а) Существуют ли на плоскости три такие точки A, B и C, что для любой точки X длина хотя бы одного из отрезков XA, XB и XC иррациональна?
б) Координаты вершин треугольника рациональны. Докажите, что координаты центра его описанной окружности также рациональны.
в) Существует ли такая сфера, на которой имеется ровно одна рациональная точка? (Рациональная точка – точка, у которой все три декартовы координаты — рациональные числа.)
а) Да, существуют. Пусть C – середина отрезка AB. Тогда XC 2 = (2XA 2 + 2XB 2 – AB 2 )/2. Если число AB 2 иррационально, то числа XA, XB и XC не могут одновременно быть рациональными.
б) Пусть (a1; b1), (a2; b2) и (a3; b3) – координаты вершин треугольника. Координаты центра его описанной окружности задаются системой уравнений:
Легко проверить, что эти уравнения линейные, а значит, решение рассматриваемой системы уравнений рационально.
в) Такая сфера существует. Например, сфера с уравнением
(x – √ 2 ) 2 + y 2 + z 2 = 2.
Точка O с координатами (0; 0; 0) – рациональная точка, лежащая на этой сфере. Остальные точки сферы иррациональные. Докажем это.
Допустим противное: пусть (x; y; z) – рациональная точка сферы, отличная от точки O. Понятно, что х отличен от 0, так как при x = 0 имеется единственное решение (0; 0; 0), которое нас сейчас не интересует. Раскроем скобки и выразим √ 2 :
x 2 – 2 √ 2 x + 2 + y 2 + z 2 = 2
√ 2 = (x 2 + y 2 + z 2 )/(2x),
чего не может быть при рациональных x, y, z и иррациональном √ 2 . Итак, О(0; 0; 0) – единственная рациональная точка на рассматриваемой сфере.
Задачи без решений
1. Докажите, что число
2. При каких целых m и n выполняется равенство (5 + 3 √ 2 ) m = (3 + 5 √ 2 ) n ?
3. Существует ли такое число а, чтобы числа а – √ 3 и 1/а + √ 3 были целыми?
4. Могут ли числа 1, √ 2 , 4 быть членами (не обязательно соседними) арифметической прогрессии?
5. Докажите, что при любом натуральном n уравнение (х + у √ 3 ) 2n = 1 + √ 3 не имеет решений в рациональных числах (х; у).
Иррациональные числа. Сравнение иррациональных и рациональных чисел.
Иррациональные числа. Числа целые, дробные, десятичные конечные и десятичные периодические носят общее название рациональных чисел; десятичные бесконечные дроби непериодические называются иррациональными числами 2) . Первые служат мерою величин, соизмеримых с единицею, вторые—мерою величин, несоизмеримых с единицею.
Иррациональное число считается известным (или данным), если указан способ, посредством которого можно находить любое число его десятичных знаков.
Два иррациональных числа (как и два рациональных) считаются равными, если они произошли от измерения одною и тою же единицею двух равных величин; из двух неравных чисел то считается большим, которое произошло от измерения большей величины. Две равные величины, конечно, должны содержать в себе одинаковое число целых единиц, одинаковое число десятых долей, одинаковое число сотых долей и т. п., поэтому равные иррациональные числа должны быть выражены одинаковыми цифрами 3) . Большая же величина должна содержать в себе большее число целых или — при равенстве целых—большее число десятых, или — при равенстве целых и десятых — большее число, сотых и т. д. Напр., число 2,745037. больше числа 2,745029. так как в первом 6-я цифра выражает число большее, чем 6-я цифра во втором, при тождественности всех предыдущих цифр.
Иррациональные числа могут быть положительными и отрицательными, смотря по тому, измеряют ли они величины, считаемые положительными, или величины, считаемые отрицательными.
186. Приближенные значения иррационального числа. Пусть нам дано какое-нибудь иррациональное число α 4) , т. е. пусть указан способ, посредством которого мы можем получить сколько угодно цифр числа α (этим способом может быть, напр., то правило, посредством которого мы находим приближенные квадратные корни с точностью до 1 /10 до 1 /100 до 1 /1000 и т. д.). Положим, мы нашли такие 5 цифр числа α:
Возьмем из этих цифр несколько первых, напр, цифры 1,41, а остальные отбросим. Тогда мы получим приближенное значение числа α, причем это значение будет с недостатком, так как 1,41
187. Определение действий над иррациональными числами. Пусть α и β будут какие-нибудь данные положительные иррациональные числа. Если эти числа даны, то это значит, что мы можем найти их приближенные значения с любою точностью. Пусть, напр., приближенные значения чисел α и β, взятые с недостатком, будут такие (мы берем приближенные значения √3 и √2 ):
| до 0,1 | до 0,01 | до 0,001 | до 0,0001 | |
| для числа α . | 1,7 | 1,73 | 1,732 | 1,7320 |
| для числа β . | 1,4 | 1,41 | 1,414 | 1,4142 |
(Соответствующие приближенные значения с избытком получаются из этих чисел посредством усиления последнего десятичного знака на 1.)
Тогда: а) сложить α и β значит найти число, которое было бы
| больше каждой из сумм: 1,7 + 1,1 . . . . =3,1 1,73 + 1,41 . . . =3,14 1,732+1,414 . . .=3,146 1,7320+1,4142 . . =3,1462 | и меньше каждой из сумм: 1,8+1,6. . . . =3,3 1,74+1,42. . . =3,16 1,733 + 1,415 . . =3,146 1,7321 + 1,4143 . .=3,1464 |
т. е. сложить числа α и β — значит найти такое третье число, которое было бы больше суммы любых приближенных их значении, взятых с недостатком, но меньше суммы любых приближенных значении, взятых с избытком.
б) Беря приближенные значения чисел α и β, указанные сейчас, мы можем сказать, что произведение α β есть число, которое
| больше каждого из произв.: 1,7•1,4. =2,38 1,73 • 1,41. =2,4393 1,732•1,114. =2,449048 1,7320 • 1,1142. =2,44939440 | и меньше каждого из произв.: 1,8•1,5. =2,70 1,74 • 1,42. =2,4708 1,733•1,415. =2,452195 1,7321 • .1,4143 . =2,44970903 |
т. е. перемножить числа α и β — значит найти такое третье число, которое было бы больше произведения их любых приближенных значений, взятых с недостатком, но меньше произведения их любых приближенных значений, взятых с избытком.
в) Возвысить иррациональное число α во вторую, третью, четвертую и т. д. степени — значит найти произведение, составленное из двух, трех, четырех и т. д. сомножителей, равных α.
г) Обратные действия определяются для иррациональных чисел так же, как и для рациональных; так, вычесть из числа α число β значит найти такое число х, чтобы сумма β + х равнялась α, и т. п.
Если одно из чисел α или β будет рациональное, то в указанных определениях прямых действий вместо приближенных значений такого числа можно брать точное число.
Произведение иррационального числа на нуль принимается, как и для чисел рациональных, равным нулю.
Действия над отрицательными иррациональными числам и производятся согласно правилам, данным для рациональных отрицательных чисел.
При более обстоятельном рассмотрении можно установить, что действия над иррациональными числами обладают теми же свойствами, какие принадлежат действиям над числами рациональными; напр., сумма и произведение обладают свойствами переместительным и сочетательным; произведение и деление, кроме того, обладают еще распределительным свойством. Свойства, выражаемые неравенствами, также сохраняются у чисел иррациональных; так, если α > β, то α + γ > β, αγ > βγ (если γ > 0) и αγ
11. Иррациональные числа
Пусть точка О — начальная точка координатной прямой и ОЕ — единичный отрезок. С помощью отрезка ОЕ можно измерить длину любого отрезка.
Измерим, например, длину отрезка ОВ (рис. 9). Отрезок ОЕ укладывается в отрезке ОВ два раза, и при этом получается остаток СВ, который меньше единичного отрезка. Значит, число 2 есть приближённое значение (с недостатком) длины отрезка О В с точностью до 1:

Чтобы получить более точный результат, разделим единичный отрезок ОЕ на 10 равных частей (рис. 10). Десятая часть отрезка ОЕ укладывается в остатке СВ три раза. При этом получается новый остаток DB, меньший десятой части отрезка ОЕ. Число 2,3 есть приближённое значение (с недостатком) длины отрезка ОВ с точностью до 0,1:

Продолжая процесс измерения, мы будем использовать сотую, тысячную и т. д. доли единичного отрезка и получать приближённые значения длины отрезка ОВ (с недостатком) с точностью до 0,01, 0,001 и т. д.
В процессе десятичного измерения могут представиться два случая: либо на каком-то шаге не получится остатка, либо остатки будут получаться на каждом шаге.
В первом случае результатом измерения окажется натуральное число или десятичная дробь, во втором случае — бесконечная десятичная дробь. Так как всякое натуральное число и всякую десятичную дробь можно записать в виде бесконечной десятичной дроби, то можно считать, что результатом десятичного измерения длины отрезка всегда является бесконечная десятичная дробь.
Пример 1. Пусть отрезок ОС равен  единичного отрезка. При десятичном измерении его длины получим число 1,75, т. е. ту же десятичную дробь, что и при делении 7 на 4. Результат измерения можно записать в виде бесконечной десятичной периодической дроби 1,75000. .
единичного отрезка. При десятичном измерении его длины получим число 1,75, т. е. ту же десятичную дробь, что и при делении 7 на 4. Результат измерения можно записать в виде бесконечной десятичной периодической дроби 1,75000. .
Пример 2. Пусть отрезок OF равен — единичного отрезка. При десятичном измерении его длины, как и при делении 8 на 3, получится бесконечная десятичная периодическая дробь 2,666. .
Пример 3. Пусть отрезок ОК равен диагонали квадрата, стороной которого служит единичный отрезок (рис. 11).

Построим на диагонали единичного квадрата новый квадрат (рис. 12). Из рисунка 12 видно, что площадь этого квадрата в два раза больше площади единичного квадрата. Значит, она равна 2. Так как отрезок ОК равен стороне нового квадрата, то длина отрезка ОК равна числу, квадрат которого равен 2.

При десятичном измерении отрезка ОК получится бесконечная десятичная дробь, которая не является периодической. Это объясняется тем, что
Предположим, что число, квадрат которого равен 2, является рациональным. Тогда это число можно представить в виде несократимои дроби  , где m — целое число, n — натуральное.
, где m — целое число, n — натуральное.
Так как  = 2, то
= 2, то  = 2 и m 2 = 2n 2 . Число 2n 2 чётное, значит, и равное ему число m 2 чётное. Но тогда и само число m является чётным (если бы число m было нечётным, то и число m 2 было бы нечётным). Поэтому число m можно представить в виде m = 2k, где k — целое число. Подставим 2k вместо m в равенство m 2 = 2n 2 . Получим: (2k) 2 = 2n 2 , 4k 2 = 2n 2 , 2k 2 = n 2 .
= 2 и m 2 = 2n 2 . Число 2n 2 чётное, значит, и равное ему число m 2 чётное. Но тогда и само число m является чётным (если бы число m было нечётным, то и число m 2 было бы нечётным). Поэтому число m можно представить в виде m = 2k, где k — целое число. Подставим 2k вместо m в равенство m 2 = 2n 2 . Получим: (2k) 2 = 2n 2 , 4k 2 = 2n 2 , 2k 2 = n 2 .
Число 2k 2 чётное, значит, число n 2 тоже чётное. Тогда и число n является четным, т. е. числитель и знаменатель дроби  — числа чётные. Это противоречит тому, что дробь
— числа чётные. Это противоречит тому, что дробь  несократима.
несократима.
Значит, неверно предположение, что число, квадрат которого равен 2, является рациональным.
Итак, десятичное измерение длин отрезков каждой точке координатной прямой, лежащей справа от начальной точки О, ставит в соответствие положительную бесконечную десятичную дробь. Наоборот, взяв произвольную положительную бесконечную десятичную дробь, мы можем найти на координатной прямой справа от точки О единственную точку А, такую, что длина отрезка ОА выражается этой дробью.
Каждому действительному числу соответствует единственная точка координатной прямой, и каждой точке координатной прямой соответствует единственное действительное число. Говорят, что между множеством действительных чисел и множеством точек координатной прямой существует взаимно однозначное соответствие.
Множество действительных чисел принято обозначать буквой R (от первой буквы латинского слова realis — реальный, существующий в действительности).
Если А(х1) и В(х2) — две точки координатной прямой, то расстояние между этими точками, т. е. длину отрезка АВ, можно найти по формуле
Бесконечные десятичные дроби могут быть периодическими и непериодическими. Бесконечные десятичные периодические дроби представляют рациональные числа. Каждое такое число можно записать в виде отношения  , где m — целое число, а n — натуральное. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает «отрицание»). Иррациональные числа нельзя представить в виде отношения
, где m — целое число, а n — натуральное. Бесконечные десятичные непериодические дроби представляют числа, не являющиеся рациональными. Их называют иррациональными числами (приставка «ир» означает «отрицание»). Иррациональные числа нельзя представить в виде отношения  , где m — целое число, а n — натуральное.
, где m — целое число, а n — натуральное.
Приведём примеры иррациональных чисел:
3,010010001. (единицы разделяются последовательно одним, двумя, тремя и т. д. нулями);
-5,020022000222. (число нулей и число двоек каждый раз увеличивается на единицу).
Иррациональным числом является число π, выражающее отношение длины окружности к диаметру:
Действительные числа, записанные с помощью бесконечных десятичных дробей, сравнивают по тем же правилам, что и конечные десятичные дроби.
Сравним, например, числа 2,36366. и 2,37011. . В этих положительных бесконечных десятичных дробях совпадают целые части и цифры десятых, а в разряде сотых у первой дроби число единиц меньше, чем у второй. Поэтому
Действительные числа можно складывать, вычитать, умножать и делить (при условии, что делитель отличен от нуля), причём действия над действительными числами обладают теми же свойствами, что и действия над рациональными числами. При выполнении действий над действительными числами в практических задачах их заменяют приближёнными значениями. Повышая точность, с которой берутся приближённые значения, получают более точное значение результата.
Пример 4. Найдём приближённое значение суммы чисел а и b,
где а =  , b = 1,7132. .
, b = 1,7132. .
Решение: Возьмём приближённые значения слагаемых с точностью до 0,1:
а ≈ 0,3, b ≈ 1,7. Получим:
а + b ≈ 0,3 + 1,7 = 2,0.
Если взять приближённые значения слагаемых с точностью до 0,01, т. е. а ≈ 0,33 и b ≈ 1,71, то получим:
а + Ь ≈ 0,33 + 1,71= 2,04.
Пример 5. Найдём длину окружности, радиус r которой равен 5 м.
Решение: Длина окружности l вычисляется по формуле l = 2πr. Взяв к ≈ 3,14, получим
l ≈ 2 • 3,14 • 5 = 31,4 (м).
Упражнения
- Приведите пример:
а) рационального числа;
б) иррационального числа.
Верно ли, что:
а) каждое рациональное число является действительным;
б) каждое действительное число является рациональным;
в) каждое иррациональное число является действительным;
г) каждое действительное число является иррациональным?
 ; 0; 0,25; -2,(3); 0,818118111. (число единиц, разделяющих восьмёрки, каждый раз увеличивается на одну); 4,2(51); 217; к укажите рациональные и иррациональные.
; 0; 0,25; -2,(3); 0,818118111. (число единиц, разделяющих восьмёрки, каждый раз увеличивается на одну); 4,2(51); 217; к укажите рациональные и иррациональные.
Сравните:

Какое из чисел больше:

Сравните числа:

Найдите расстояние между точками М и К координатной прямой, если:

Какая из точек С или D координатной прямой ближе к точке М, если:
а) С (4,514), D (-1,9368. ), М (1,304);
б) С (-2,4815. ), D (11,454), М (4,586).
Расположите в порядке возрастания числа
4,62; 3,(3); -2,75. ; -2,63. .
Расположите в порядке убывания числа
1,371. ; 2,065; 2,056. ; 1,(37); -0,078. .
Какие целые числа расположены между числами:
а) -3,168. и 2,734. ;
б) -5,106. и -1,484. ;
в) -4,06 и -1,601;
г) -1,29 и 0,11?
Найдите приближённое значение выражения а + b, где а = 1,0539. и b = 2,0610. округлив предварительно а и b:
а) до десятых;
б) до сотых;
в) до тысячных.
Найдите приближённое значение выражения а — b, где а = 59,678. и b = 43,123. округлив предварительно а и b:
а) до десятых;
б) до сотых.

Найдите значение выражения:

 проходит через точку А (4; -0,5). Найдите k и постройте этот график.
проходит через точку А (4; -0,5). Найдите k и постройте этот график.Иррациональные числа, определение, примеры.
Материал этой статьи представляет собой начальную информацию про иррациональные числа. Сначала мы дадим определение иррациональных чисел и разъясним его. Дальше приведем примеры иррациональных чисел. Наконец, рассмотрим некоторые подходы к выяснению, является ли заданное число иррациональным или нет.
Навигация по странице.
- Определение и примеры иррациональных чисел.
- Является ли данное число иррациональным?
Определение и примеры иррациональных чисел
При изучении десятичных дробей мы отдельно рассмотрели бесконечные непериодические десятичные дроби. Такие дроби возникают при десятичном измерении длин отрезков, несоизмеримых с единичным отрезком. Также мы отметили, что бесконечные непериодические десятичные дроби не могут быть переведены в обыкновенные дроби (смотрите перевод обыкновенных дробей в десятичные и обратно), следовательно, эти числа не являются рациональными числами, они представляют так называемые иррациональные числа.
Так мы подошли к определению иррациональных чисел.
Числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби, называются иррациональными числами.
Озвученное определение позволяет привести примеры иррациональных чисел. Например, бесконечная непериодическая десятичная дробь 4,10110011100011110000… (количество единиц и нулей каждый раз увеличивается на одну) является иррациональным числом. Приведем еще пример иррационального числа: −22,353335333335… (число троек, разделяющих восьмерки, каждый раз увеличивается на две).
Следует отметить, что иррациональные числа достаточно редко встречаются именно в виде бесконечных непериодических десятичных дробей. Обычно они встречаются в виде корней, степеней, логарифмов и т.п., а также в виде специально введенных букв. Самыми известными примерами иррациональных чисел в такой записи являются арифметический квадратный корень из двух , число «пи» π=3,141592… , число e=2,718281… и золотое число .
Иррациональные числа также можно определить через действительные числа, которые объединяют рациональные и иррациональные числа.
Иррациональные числа – это действительные числа, не являющиеся рациональными.
Является ли данное число иррациональным?
Когда число задано не в виде десятичной дроби, а в виде некоторого числового выражения, корня, логарифма и т.п., то ответить на вопрос, является ли оно иррациональным, во многих случаях достаточно сложно.
Несомненно, при ответе на поставленный вопрос очень полезно знать, какие числа не являются иррациональными. Из определения иррациональных чисел следует, что иррациональными числами не являются рациональные числа. Таким образом, иррациональными числами НЕ являются:
- натуральные числа;
- целые числа;
- обыкновенные дроби;
- смешанные числа;
- конечные и бесконечные периодические десятичные дроби.
Также не является иррациональным числом любая композиция рациональных чисел, связанных знаками арифметических операций (+, −, ·, :). Это объясняется тем, что сумма, разность, произведение и частное двух рациональных чисел является рациональным числом. Например, значения выражений и являются рациональными числами. Здесь же заметим, что если в подобных выражениях среди рациональных чисел содержится одно единственное иррациональное число, то значение всего выражения будет иррациональным числом. Например, в выражении число — иррациональное, а остальные числа рациональные, следовательно — иррациональное число. Если бы было рациональным числом, то из этого следовала бы рациональность числа , а оно не является рациональным.
Если же выражение, которым задано число, содержит несколько иррациональных чисел, знаки корня, логарифмы, тригонометрические функции, числа π , e и т.п., то требуется проводить доказательство иррациональности или рациональности заданного числа в каждом конкретном случае. Однако существует ряд уже полученных результатов, которыми можно пользоваться. Перечислим основные из них.
Доказано, что корень степени k из целого числа является рациональным числом только тогда, когда число под корнем является k-ой степенью другого целого числа, в остальных случаях такой корень задает иррациональное число. Например, числа и — иррациональные, так как не существует целого числа, квадрат которого равен 7 , и не существует целого числа, возведение которого в пятую степень дает число 15 . А числа и не являются иррациональными, так как и .
Что касается логарифмов, то доказать их иррациональность иногда удается методом от противного. Для примера докажем, что log23 является иррациональным числом.
Допустим, что log23 рациональное число, а не иррациональное, то есть его можно представить в виде обыкновенной дроби m/n . Свойства логарифма и свойства степени позволяют записать следующую цепочку равенств: . Последнее равенство невозможно, так как в его левой части нечетное число, а в правой части – четное. Так мы пришли к противоречию, значит, наше предположение оказалось неверным, и этим доказано, что log23 — иррациональное число.
Заметим, что lna при любом положительном и отличном от единицы рациональном a является иррациональным числом. Например, и — иррациональные числа.
Также доказано, что число e a при любом отличном от нуля рациональном a является иррациональным, и что число π z при любом отличном от нуля целом z является иррациональным. К примеру, числа — иррациональные.
Иррациональными числами также являются тригонометрические функции sin , cos , tg и ctg при любом рациональном и отличном от нуля значении аргумента. Например, sin1 , tg(−4) , cos5,7 , являются иррациональными числами.
Существуют и другие доказанные результаты, на мы ограничимся уже перечисленными. Следует также сказать, что при доказательстве озвученных выше результатов применяется теория, связанная с алгебраическими числами и трансцендентными числами.
В заключение отметим, что не стоит делать поспешных выводов относительно иррациональности заданных чисел. К примеру, кажется очевидным, что иррациональное число в иррациональной степени есть иррациональное число. Однако это не всегда так. В качестве подтверждения озвученного факта приведем степень . Известно, что — иррациональное число, а также доказано, что — иррациональное число, но — рациональное число. Также можно привести примеры иррациональных чисел, сумма, разность, произведение и частное которых есть рациональные числа. Более того, рациональность или иррациональность чисел π+e , π−e , π·e , π π , π e и многих других до сих пор не доказана.






