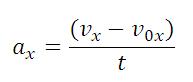Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.

Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.

Кинематика

О чем эта статья:

Прямолинейное равномерное движение

Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.

Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.

Мы можем охарактеризовать это движение следующими величинами.

Скалярные величины (определяются только значением)

• Время — в международной системе единиц СИ измеряется в секундах [с].
• Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].

Векторные величины (определяются значением и направлением)

• Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
• Путь — вектор, проведенный из начальной точки пути в конечную [м].

Проецирование векторов

Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.

Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.

Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.

Скорость может определяться по вектору перемещения и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.

Скорость

→ →
V = S/t

→
S — перемещение [м]

Средняя путевая скорость

V ср.путевая = S/t

V ср.путевая — средняя путевая скорость [м/с]

В чем разница между перемещением и путем?

Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача

Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.

Решение:

Возьмем формулу средней путевой скорости

V ср.путевая = S/t

V ср.путевая = 210/2,5 = 84 км/ч

Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч

Уравнение движения

Основной задачей механики является определение положения тела в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).

Уравнение движения

x(t) = x0 + vxt

x(t) — искомая координата [м]

x0 — начальная координата [м]

vx — скорость тела в данный момент времени [м/с]

t — момент времени [с]

Уравнение движения при движении против оси

x(t) = x0 — vxt

x(t) — искомая координата [м]

x0 — начальная координата [м]

vx — скорость тела в данный момент времени [м/с]

t — момент времени [с]

Графики

Изменение любой величины можно описать графически. Вместо того, чтобы писать множество значений, можно просто начертить график — это проще.

В видео ниже я рассказываю, как строить графики кинематических величин и зачем они нужны.

Прямолинейное равноускоренное движение

Чтобы разобраться с тем, что за тип движения в этом заголовке, нужно ввести новое понятие — ускорение.

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. В международной системе единиц СИ измеряется в метрах, деленных на секунду в квадрате.

То есть прямолинейное движение — это движение с ускорением по прямой линии, движение, при котором скорость тела меняется на равную величину за равные промежутки времени.

Уравнение движения и формула конечной скорости

Основная задача механики не поменялась по ходу текста — определение положения тела в данный момент времени. У равноускоренного движения в уравнении

Уравнение движения для равноускоренного движения

x(t) — искомая координата [м]

x0 — начальная координата [м]

v0x — начальная скорость тела в данный момент времени [м/с]

ax — ускорение [м/с^2]

Для данного процесса также важно уметь находить конечную скорость. Это часто упрощает решение задач. Она находится по формуле

Формула конечной скорости

→ →
v = v0 + at

→
v — конечная скорость тела [м/с]

v0 — начальная скорость тела [м/с]

→
a — ускорение [м/с^2]

Задача

Найдите местоположение автобуса через 0,5 часа после начала движения, разогнавшегося до скорости 60 км/ч за 3 минуты.

Решение:

Сначала найдем ускорение автобуса. Его можно выразить из формулы конечной скорости:

Так как автобус двигался с места, v0 = 0. Значит

Время дано в минутах, переведем в часы, чтобы соотносилось с единицами измерения скорости.

3 минуты = 3/60 часа = 1/20 часа = 0,05 часа

a = v/t = 60/0,05 = 1200 км/ч^2

Теперь возьмем уравнение движения.

Начальная координата равна нулю, начальная скорость, как мы уже выяснили — тоже. Значит уравнение примет вид:

Ускорение мы только что нашли, а вот время будет равно не 3 минутам, а 0,5 часа, так как нас просят найти координату в этот момент времени.

x = 1200*0,5^2/2 = (1200*0,5^2)/2 = 150 км

Ответ: через полчаса координата автобуса будет равна 150 км.

Графики

Мы уже знаем, что такое графики функций и зачем они нужны. Для прямолинейного равноускоренного движения графики будут отличаться. Об этом — в видео ниже.

Движение по вертикали

Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с^2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).

Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с^2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с^2.

И кому же верить?

Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с^2.

Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.

Помните о том, что свободное падение — это не всегда движение по вертикали. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела, когда тело движется вокруг некоторой точки. Очень важно разделить движение по окружности и вращение тела.

При вращательном движении тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги. Это очень похоже на равномерное движение, только в данном случае мы имеем дело с дугами.

При движении по окружности тело двигается вокруг одной точки, а при вращении — все точки тела движутся вокруг оси вращения.

В видеролике ниже рассказано про ускорение при криволинейном движении. Оно складывается из двух составляющих — нормальной и тангенциальной. При равномерном движении по окружности тангенциальная составляющая отсутствует, остается нормальная, которую мы в данном случае называем центростремительной.

Центростремительное ускорение

При движении по окружности модуль скорости постоянен, а вот направление скорости постоянно меняется. За изменение направления скорости отвечает центростремительное ускорение.

Центростремительное ускорение

aц = v^2/R

aц — центростремительное ускорение [м/с^2]

R — радиус окружности [м]

Задачка

Мотоцикл движется по закруглённому участку дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение мотоцикла?

Решение:

Возьмем формулу центростремительного ускорения тела

В условии задачи скорость дана в километрах в час, а радиус в метрах. Значит, нужно перевести скорость в м/с, чтобы избежать коллапса в решении.

Теперь можно подставить значения в формулу:

aц = 10^2/120 = 100/120 = 10/12 ≃ 0,83 м/с^2

Ответ: центростремительное ускорение мотоциклиста равно 0,83 м/с^2

ИНФОФИЗ — мой мир.

Весь мир в твоих руках — все будет так, как ты захочешь

Весь мир в твоих руках — все будет так, как ты захочешь

• Главная
• Мир физики
  • Физика в формулах
  • Теоретические сведения
  • Физический юмор
  • Физика вокруг нас
  • Физика студентам
    • Для рефератов
    • Экзамены
    • Лекции по физике
    • Естествознание
• Мир астрономии
  • Солнечная система
  • Космонавтика
  • Новости астрономии
  • Лекции по астрономии
  • Законы и формулы — кратко
• Мир психологии
  • Физика и психология
  • Психологическая разгрузка
  • Воспитание и педагогика
  • Новости психологии и педагогики
  • Есть что почитать
• Мир технологий
  • World Wide Web
  • Информатика для студентов
    • 1 курс
    • 2 курс
  • Программное обеспечение компьютерных сетей
    • Мои лекции
    • Для студентов ДО
    • Методические материалы

• Физика школьникам
• Физика студентам
• Астрономия
• Информатика
• ПОКС
• Арх ЭВМ и ВС
• Методические материалы
• Медиа-файлы
• Тестирование

Как сказал.

Информация в чистом виде ‒ это не знание. Настоящий источник знания ‒ это опыт.

Альберт Эйнштейн

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 03. Лекция 03. Виды механического движения

• » onclick=»window.open(this.href,’win2′,’status=no,toolbar=no,scrollbars=yes,titlebar=no,menubar=no,resizable=yes,width=640,height=480,directories=no,location=no’); return false;» rel=»nofollow»> Печать
• E-mail

Виды движения (равномерное, равноускоренное) и их графическое описание

По форме траектории движение делится на криволинейное (траектория движения тела кривая линия) и прямолинейное (траектория движения тела прямая линия).

При движении тела по прямолинейной траектории модуль вектора перемещения всегда совпадает с пройденным путём. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути

Равномерное прямолинейное движение.

Прямолинейным равномерным движением называют движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.

Скорость равномерного прямолинейного движения — это физическая векторная величина, равная отношению перемещения тела S за любой промежуток времен к значению этого промежутка t:

Скорость — это физическая величина, показывающая быстроту изменения координаты.

Единицы измерения скорости — метры в секунду [1 м/с]

Уравнение равномерного движения ( перемещение тела при равномерном движении):

Уравнение координаты тела:

Обозначения:

х— координата движущегося тела

х₀ — начальная координата движущегося тела

v _ср-Средняя скорость равномерного прямолинейного движения

v_х — Скорость равномерного прямолинейного движения

S — Перемещение тела (расстояние, на которое передвинулось тело)

t — Промежуток времени перемещения (время)

Графическое представление равномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) — прямая линия, которая лежит на оси времени.

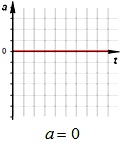
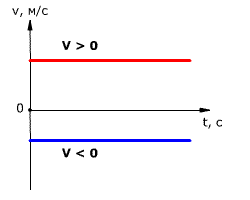
Зависимость скорости от времени. Так как тело движется прямолинейно и равномерно ( v=const), т.е. скорость со временем не изменяется, то график с зависимостью скорости от времени v(t) — прямая линия, параллельная оси времени.

Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

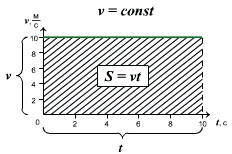
Правило определения пути по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.

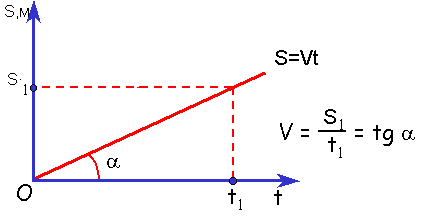
Зависимость перемещения от времени. График s(t) — наклонная линия :

Зависимость координаты от времени. График х(t) — наклонная линия :

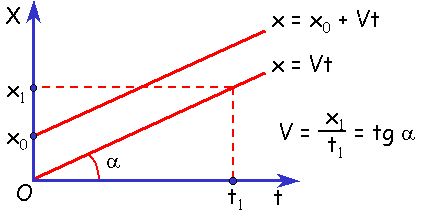
Из графика видно, что проекция скорости равна:

Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.

Правило определения скорости по графику s(t) и x(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Неравномерное прямолинейное движение.

Равномерное движение это движение с постоянной скоростью. Если скорость тела меняется, говорят, что оно движется неравномерно.

Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют неравномерным илипеременным движением.

Для характеристики неравномерного движения вводится понятие средней скорости.

Средняя скорость движения равна отношению всего пути, пройденного материальной точкой к промежутку времени, за который этот путь пройден.

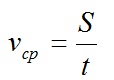
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость за бесконечно малый промежуток времени Δt:

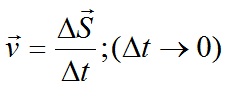
Мгновенной скоростью переменного движения называют скорость тела в данный момент времени или в данной точке траектории.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке.

Различие между средней и мгновенной скоростями показано на рисунке.

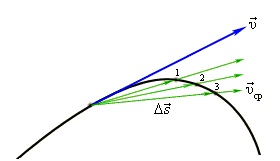
Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называютравноускоренным или равнопеременным движением.

Ускорение — это векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:

v_х — конечная скорость тела при равноускоренном движении по прямой

a — ускорение тела

t — время движения тела

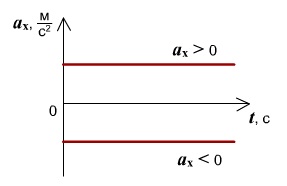
Ускорение показывает, как быстро изменяетcя скорость тела. Если ускорение положительно, значит скорость тела увеличивается, движение ускоренное. Если ускорение отрицательно, значит скорость уменьшается, движение замедленное.

Единица измерения ускорения в СИ [ м/с 2 ].

Ускорение измеряют акселерометром

Уравнение скорости для равноускоренного движения:

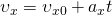
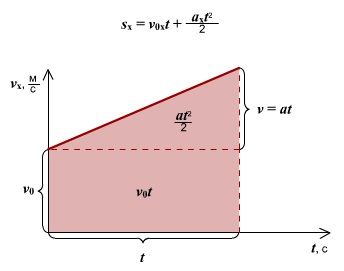
Уравнение равноускоренного прямолинейного движения (перемещение при равноускоренном движении):

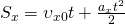
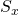— Перемещение тела при равноускоренном движении по прямой

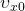— Начальная скорость тела

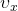— Скорость тела при равноускоренном движении по прямой

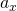— Ускорение тела

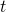— Время движения тела

Еще формулы, для нахождения перемещения при равноускоренном прямолинейном движении, которые можно использовать при решении задач:

— если известны начальная, конечная скорости движения и ускорение.

— если известны начальная, конечная скорости движения и время всего движения

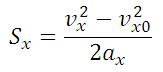
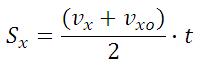
Графическое представление неравномерного прямолинейного движения

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают:

v(t) — изменение скорости со временем

S(t) — изменение перемещения (пути) со временем

a(t) — изменение ускорения со временем

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) — прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении скорость изменяется, согласно линейной зависимости .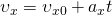

Графиком является наклонная линия.

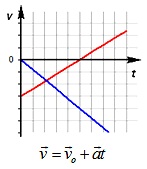
Правило определения пути по графику v(t): Путь тела — это площадь треугольника (или трапеции) под графиком скорости.

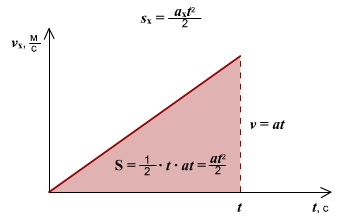
Правило определения ускорения по графику v(t): Ускорение тела — это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

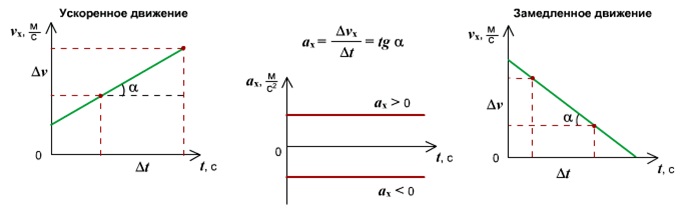
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратичной зависимости

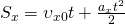
В координатах зависимость имеет вид .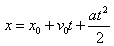

Равномерное и равноускоренное прямолинейное движение. Материальная точка.

Опубликовано 29.09.2020Образование

Равномерное и равноускоренное прямолинейное движение. Материальная точка.

В данной статье рассмотрены наиболее популярные задания ЕГЭ по физике 2020, которые могут встретиться в КИМах. Они помогут вам более глубоко и подробно ознакомиться с темами ЕГЭ из раздела механики, данные темы рассмотрены в соответствии с кодификатором элементов содержания и требований к подготовке выпускников.

Итак, перейдём к рассмотрению. Довольно часто в ЕГЭ по физике встречаются задачи на движение, поэтому просим заранее запоминать необходимые определения и формулы.

Равномерное прямолинейное движение – движение, имеющее постоянную скорость. При таком движении тело должно передвигаться по прямой, за одинаковые промежутки времени пройдёт равные пути.

Неравномерное движение – это движение, в котором за одинаковый промежуток времени сделают разные перемещения. В таком движении скорость будет изменяться с отпрядённым течением времени.

Равнопеременное движение – движение, при котором скорость тела изменится за одинаковое время. То есть такой вид движения включает в себя постоянное ускорение.

Равноускоренное движение – движение, в соответствии с которым скорость постоянно увеличивается.

Равнозамедленное – движение, в соответствии с которым скорость уменьшается.

Рассмотрим прямолинейное движение. Для его описания требуется в начале движения измерить координаты тела в разные промежутки времени.

Для описания прямолинейного движения в определённой системе отсчёта нужно в начале движения воспользоваться часами и измерить координаты тела.

Материальная точка

Также распространённой темой в ЕГЭ по физике является материальная точка, дополнительно рассмотрим здесь её траекторию, перемещение, путь и сложение перемещений.

Механическое движение считается более простым. Дадим определение механическому движению – это процесс, когда тело меняет своё положение по отношению к другим телам.

Рассмотрим основные характеристики движения тела в разное время:

— Путь, который пройден;

— И другие характеристики, используемые в целях решения заданий, если такие задания связаны с движением тел в пространстве.

Рассмотрим пример. При запускании спутника на другую планету, ученые рассчитывают расстояние до местонахождения исследуемой планеты по отношению к Земле. Также выясняют скорость планеты, её направление и траекторию движения. Положение точек определяют с помощью координатной прямой ил системы координат. Посмотрим пример (рис. 1):

Здесь возникает вопрос как же изобразить объёмное тело с множеством точек, имеющих координаты. Рассмотрим рисунок (рис. 2):

На этом этапе возникают и другие немаловажные вопросы, такие как: что является скоростью планеты, если она одновременно вращается вокруг своей оси. Это обусловлено тем, что скорость различных точек отличается по своему направлению и модулю. Следует учитывать, что чем меньше расстояние точки к оси, тем меньше будет её скорость.

Обычно разные тела рассматривают в качестве материальных точек, при условии, что расстояние, которое проходят данные точки больше размера самих тел.

Формулы, которые необходимо использовать при решении задач на данную тему:

— s = v0t + ( at^2 / 2 );

Рассмотрим пример решения задачи.

Условие задачи: По прямой движется материальная точка. Скорость в соответствии с временем равна: v ( t ) = t^3 – 2t.

Найти ускорение, при t = 3.

v ( t ) = t^2 – 2t = 3 * t^2 – 2.

v3 = 3 * 3^2 – 2 = 25.

Ответ: a ( 3 ) = 25.

Обратим внимание на то, что материальных точек не существует. Это понятие введено в целях решения задач с наиболее точными результатами.

Радиусом-вектором материальной точки является вектор, который соединяет координатную плоскость с самой материальной точкой. Рассмотрим пример (рис. 3).

Траектория – это невидимая линия, которую можно представить на графике, она будет описывать точку в процессе движения.

Путь – длина невидимой линии.

Перемещением является вектор, который соединяет положение тела в начале и в конце движения.

Нужно помнить, что перемещение может быть нулевое, даже при прохождении большого пути. Примером будет служить поход в школу (10 км), далее – в магазин (15 км) и обратно домой – 20 км. Пройденный путь составляет 45 км, но перемещение = 0. Это объясняется тем, что путь домой совпадает с началом и концом движения. Вектор, который соединяет начало и конец движения равен нулю.

В случае, когда мы знаем координаты точек, для определения их перемещения применяем формулы:

Обратите внимание на то, что путь является скалярной величиной, а вектор с перемещением – векторной.

Если мы с объектом в разных системах отсчёта, воспользуемся ещё одной формулой: r (t) = r (t) + R (t).

Скорость материальной точки

Если движение рассматриваемой в условии задачи точки является прямолинейным, следует применять формулу: u = s / t. В случае, когда скорость изменяет направление движения, то она постоянна в определённом времени.

u = ds / dt = s, ds – расстояние, dr – перемещение.

Путь – s, который пройден за промежуток времени t = t2 – t1, будет равен интегралу u по t.

U – вектор, который направлен к траектории. Расстояние и величина перемещения, которые пройдены за небольшой промежуток времени равны, то есть ds = dr.

Формула скорости в векторном виде: u = dr / dt.

Средняя скорость движения высчитывается по формуле: u ср = r / t.

При описании движения материальных точек используют координаты х, у, z. В начале вычисляют проекции на осях: ux = dx / dt = x1, uy = dy / dt = y1, uz = dz / dt = z1.

Ускорение материальной точки

Часто в ЕГЭ по физике встречаются задачи на ускорение, оно показывает, как быстро меняется скорость материальной точки. Применяем формулу: а = du / dt, где du – изменение скорости за небольшое время. Также можно вывести формулу тангенциального ускорения: а = at + an. Такой вид ускорения возникает в случае изменения величины скорости, оно будет равно производной скорости и времени: aт = du / dt = u. При движении со скоростью аt = 0: an = u^2 / p, р – кривизна в точке, её радиус.

В случае, когда траекторией точки является окружность, радиус будет такой же как у окружности, то есть p = R.

Тангенциальное ускорение всегда направляется к траектории с помощью касательной.

Также в процессе подготовки к сдаче экзамена рекомендуем прочесть методические рекомендации ЕГЭ по физике 2020 и просмотреть демонстрационные варианты, размещённые в открытом доступе. С помощью них вы сможете ознакомить со структурой КИМов, количеством содержащихся заданий, их формулировками и уровнем сложности. Задания из демонстрационных вариантов, как правило, не попадаются на ЕГЭ, встречаются обычно похожие, с разными условиями задач.

В завершение отметим, что ознакомившись с данной статьёй, материалами, изложенными в ней, а также дополнительными рекомендациями, вы будете готовы к ЕГЭ по физике. Встретив в КИМах задания подобных планов, вам не составит труда решить их. Таким образом, мы рассмотрели и разобрали тему и решение задач, наиболее часто встречающихся на едином государственном экзамене.