Функция и производная: что это и чем они отличаются

Функция и производная: что это и чем они отличаются

Основной базой для всех учений, познающих мир, является математика. Точная наука использует формализованный язык и изучает порядок, структуру и отношения на выбранных абстрактных объектах. Не всем обучающимся нравится математика из-за её сложности и запутанности, а, скорее всего, из-за непонимания. Прочные изменения в отношении к математике потребуют увлеченности, сосредоточенности, последовательности, даже упрямства и, главное, практических решений. В изучении важно шаг за шагом разбираться изначально в простом и постепенно переходить к более сложному, не оставляя непонятного и непродуманного.

Существуют много различных разделов математики уже достаточно изученных и появившихся недавно. Далее рассказывается об азах математического анализа – основных начальных понятиях, определениях и правилах исследования простых функций одной переменной, производной и дифференцирования.

У студентов начальных курсов вузов появился афоризм: «Математика становится по-настоящему сложной, когда из неё пропадают цифры». И действительно, к пониманию некоторых определений и законов математической науки приближаются путем решения по правилам на конкретных примерах.

Основные определения

Начнем с терминологии – с простых общих смысловых значений первичных определений:

• Переменная – величина или символ, может принимать любое из ряда значений в

определенной области (вес или рост ребенка)

• Функция – назначение, работа, деятельность, определенное действие над переменной, обозначим f(x) (зависимость веса ребенка от его роста)
• Предел – лимит, граница, край (горизонт – граница обзора)
• Производная – образованная, вторичная, проистекшая от другого, обозначим f’(x) (скорость при движении)
• Дифференциал – разность, различие, разделение.

Функция это просто

Функция – это результат того, что она делает с переменной, что является итогом вычисления. Это взаимосвязь элементов, при которой изменение одного переменного обуславливает изменение в другом. Разделяют f(x) на простые и сложные.

Для отображения зависимостей используются следующие способы: алгебраический, графический, табличный, логический и даже программные.

Определяют числовые зависимости алгебраически с использованием символов переменных, равенств и неравенств (≤ и >), строится уравнение вида: y = f(x), здесь x — переменная или аргумент, а y или f(x) — функция. Каждому конкретному значению переменной x из допустимой области определения соответствует определенное значение y для заданной f (x).

На рисунке ниже представлены простые графики 3-х различных соотношений. Видно, что в f(x) 3 получается наибольшее значение y при х конкретном, в f(x) 1 — наименьшее.

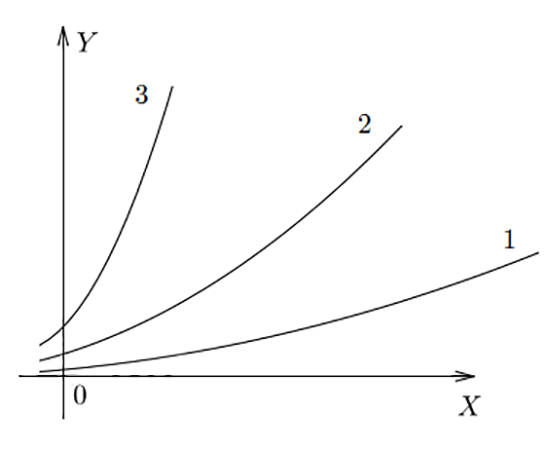
Различают следующие элементарные выражения: линейная (прямая), квадратичная (парабола), кубическая, гипербола, показательная, логарифмическая, тригонометрические (приведены в таблице ниже).

Для анализа каждого вида f(x) определяют присущие им свойства (перечислены ниже), для этого используют понятия производной и дифференциала.

Производная функции

Производная – оператор, который для исходной f(x) по законам дифференцирования ставит в соответствие другую функцию, она характеризует изменение первичной f(x) аргумента x в некоторой точке. Для её детального понимания следует разобраться с более сложными определениями предела зависимости и дифференцирования.

Предел – это определение динамическое. Выражение, что x стремится к n, понимают так – х обретает значения, которые близко приближаются к п и разнятся на мизерную величину.

Дифференциал – малое изменение какой-то величины. Приращение назовем дельтой.

Производной для f(x) в точке является предел деления дельты функции к дельте переменной в данной точке, если последняя стремится к 0.

Характеристика скорости изменения зависимости в данной точке, геометрически её можно показать, как значение tg угла наклона альфа касательной к функции.

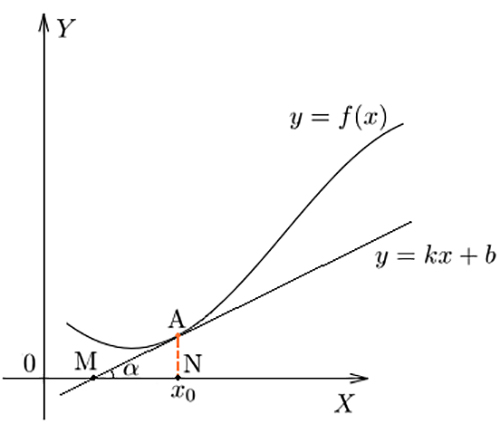
Зависимость называется дифференцируемой, если определена f’(x). Нахождение производной называется дифференцированием. Правила вычисления f’(x) и соответствия f’(x) от элементарных f(x) приведены в таблице ниже

Производная функции также функция

Каждая зависимость имеет определенные свойства, зная и исследуя их можно анализировать характер состояния и изменения f(x).

• Данные промежутков определений и промежутков значений.
• Нулевые значения f(x)
• Функция возрастает или убывает в некоторых промежутках.
• Точки MAX и MIN функции, есть ли перегиб.
• Четная или нечетная f(x)
• Ограниченная и неограниченная функция.
• Есть ли асимптоты.
• Периодичность f(x).

Функции и производные

При установлении характеристик зависимости с помощью производной используют взаимосвязи свойств f’(x) со свойствами f(x) и наоборот. На графике функции легко определяются характеристики f’(x), и наоборот по графику f’(x) понимаются характеристики первичной f(x). Фиксируя сущность каждой особенности функции, исследуют и устанавливают цепочку связей. Для определения асимптот в графиках используют понятие пределов.

Ниже приведены некоторые характеристики и зависимости f’(x) от f(x):

• При возрастании f(x) на промежутке, f’(x) положительна.
• В случае убывания f(x) на промежутке, f’(x) отрицательна.
• При наличии f(x) точки MAX, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с + на -.
• При наличии f(x) точки MIN, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с – на +.
• При перегибе в Е графика f(x) значение f’(x) не поменяло в точке знак, f’(x)=0.

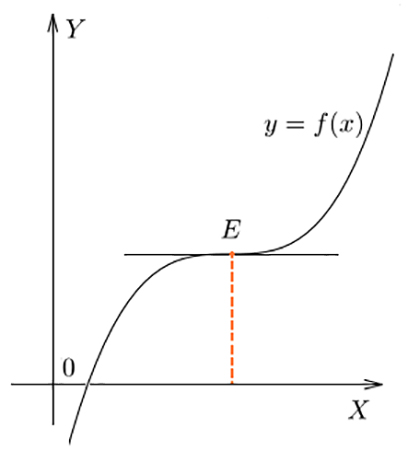
Перегиб в точке Е графика функции

Для исследования f(x) составляют схему, где каждый шаг строится по определенному алгоритму вычислений и анализа взаимосвязей составляющих элементов.

Различия функции и производной

Правила сложения и вычитания f(x) одинаковы с правилами этих действий при дифференцировании. Но правила нахождения f’(x) при действиях умножения и деления функций другие (как в таблице).

Функция первична, а производная – произведенная вторичная математическая операция, у них в большинстве случаев разные характеристики.

Точку перегиба непрерывной зависимости находят по её второй производной, должен меняться её знак в районе точки х0.

Есть такие типы функций не имеющих f’(x) в точке x0 (разрывные). В выражении ln(|x|-1) не определена в точке x0=1 производная.

Есть выражения «по модулю» аналогичные y=|x|, которые имеет излом в х0.

Для подобных зависимостей применяются лишь частично (на промежутках области определения) способы исследования их свойств с помощью производных и не всегда возможен переход от свойств f’(x) к свойствам первичной.

Нигде не обойтись без исключений из правил, и даже в математике. С целью разбора и закрепления изложенного материала обязательно следует порешать примеры, напрактиковаться, набраться опыта с пределами, дифференциалами и производными и смело переходить к интегралам.

Решение производной для чайников: определение, как найти, примеры решений

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

• Контрольная работа от 1 дня / от 100 р. Узнать стоимость
• Дипломная работа от 7 дней / от 7950 р. Узнать стоимость
• Курсовая работа 5 дней / от 1800 р. Узнать стоимость
• Реферат от 1 дня / от 700 р. Узнать стоимость

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

О производных

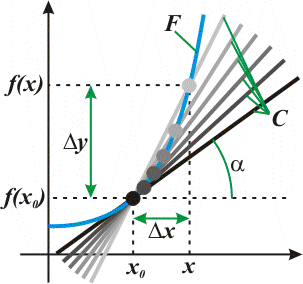
Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие. Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. А что мне с производной? Ну, знаю я «предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует» — и что? В общем, не понимал я это дело. И не любил.
И только значительно позже, уже в ВУЗе, когда оказалось, что ни одна мало-мальски важная задача по физике, электротехнике, системам автоматического управления, мат.анализу и многим другим предметам без производных не решается — я понял, какая это важная вещь — знание не только текущего положения дел, но и динамики их изменения. Казалось бы, и что статья с таким началом может делать в этом блоге?

А вот что. Представьте себе двух людей. Пусть их будут звать Коля и Петя.

Коля и Петя — одного возраста, пола, с одинаковым образованием и работают в одной и той же фирме, на должностях одного уровня и получают одинаковую зарплату.

Какие на основании данной вводной можно сделать выводы? Можно ли сказать, что их жизнь складывается одинаково? Можно ли утверждать, что они одинаково довольны в финансовом и личном плане? Можно ли сказать, что их карьеры строятся схожим образом?
Конечно же, нифига подобного!
Дело в том что Коля — всегда был очень умён, трудолюбив и раньше, до наблюдаемого нами момента, его карьера шла очень хорошо. Он был начальником начальника Пети и зарабатывал раз в 25 больше. Но потом в его жизни что-то поменялось — может жена ушла, может в секту попал, а может пить начал. Или всё вместе. Блеск в глазах пропал, после двух сорванных проектов в должности его понизили и на горизонте замаячил злорадный силуэт увольнения.
А вот Петя — гением никогда не был. Он был обычным неглупым трудягой, который честно работал. Без героических свершений и позорных провалов. Его карьера медленно и плавно двигалась в гору и кресло начальника отдела уже, в принципе, было готово принять в себя его попу.

Вот это и есть важность понимания динамики процесса. Глянем для закрепления материала на еще одну ситуацию.
У нас есть Маша, Даша и Наташа.

Они, как и их друзья Коля и Петя, полностью идентичны в своём текущем состоянии (возраст, работа, зарплата, семейное положение ну и т.д.). Более того, мы даже кое-что знаем об их прошлом. Никто из них никогда не забирался выше текущего места в жизни, никаких форс-мажоров у них не было, и у нас есть еще одна важная вещь — информация о некотором моменте в прошлом (скажем, год назад). И согласно этой информации — опять таки, все объективные параметры этих девушек были равны. Вернёмся к нашим вопросам. Как на счёт оценки положения дел у этих дам? Можно ли говорить об одном уровне карьерного роста, амбициях, достижениях и о том, где каждая из них будет через 5 лет?
И, конечно же, опять — нифига подобного!

Глянем вот на этот график:

Даша — стабильный середнячок. Она растет в меру своих сил, этих сил на все хватает и будет хватать.
Наташа — пока еще справляется, но уже без былого энтузиазма. Большего, чем сейчас, ей не хочется и не светит. Это почти её предел.
Маша — сильная и амбициозная личность. Текущая точка — просто досадное недоразумение, первая ступенька в лестнице её карьеры. Ну просто времени еще было мало и выше забраться пока не удалось. Но обязательно удастся и на это будут брошены все силы.

К чему это я?

1. Частенько в разговорах между давно не встречавшимися или только познакомившимися людьми проскакивают фразы в духе:

• А где работаешь?
• А кем?
• Сколько получаешь?

и т.д.
Люди получают ответы на эти вопросы и судят по ним о собеседнике. А ведь это всего лишь «положение дел в данной точке», которое, как мы уже выяснили, информации несёт мало. Не судите поспешно.

2. Иногда человек смотрит сам на себя со стороны и приходит к выводу, что, мол «я ничтожество, нищий и убогий, а еще дурак и бездарь» или наоборот «я всего добился, я крут, бел и пушист». В первом случае люди зря ставят на себе крест и лезут в петлю, хотя вполне еще можно выбраться, во втором — слишком рано расслабляются и почивают на лаврах, хотя из-за какого-нибудь угла легко может подкрасться кризис, капец и конец света.

3. Посмотрите на графики сверху. Где Ваш? А Вы уверены? А почему? А Вы по нему двигаетесь? А на Вашей должности и в Вашей компании вообще по нему можно двигаться? Что Вас останавливает? Хотите ли Вы через 5 лет быть в той же точке? А на том же графике?

Производная, основные определения и понятия

Данная статья рассматривает основные понятия, для решения задач с производными с одной переменной.

Пусть х – это аргумент функции f ( x ) и ∆ x возьмем малое число, не равное 0 . Значение ∆ x называют приращением аргумента функции и читают как «дельта икс». На рисунке видно, что красная линия относится для изменений аргумента от значения х до x + ∆ x .

Когда значение аргумента x 0 переходит к x 0 + ∆ x , тогда и значение функции меняется от f ( x 0 ) до f ( x 0 + ∆ x ) , если имеется условие монотонности функции из отрезка [ x 0 ; x 0 + ∆ x ] . Приращение функции f ( x ) – это разность f ( x 0 + ∆ x ) — f ( x 0 ) = ∆ f ( x ) приращения аргумента. Это приведено на рисунке, расположенном ниже.

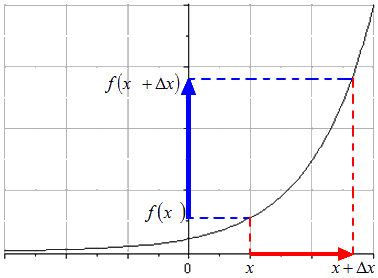
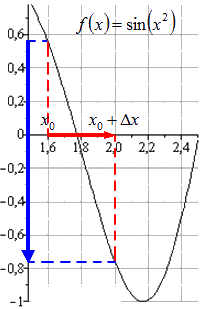
Для полного уяснения рассмотрим на конкретном примере. Если взять функцию f ( x ) = sin ( x 2 ) , тогда следует зафиксировать точку x 0 = 1 . 6 и приращение аргумента вида ∆ x = 0 . 4 . Тогда получим, что приращение функции при переходе от x 0 = 1 . 6 к x 0 + ∆ x = 1 . 6 + 0 . 4 = 2 будет равно:

∆ f ( x ) = ∆ sin ( x 2 ) = sin ( ( x 0 + ∆ x ) 2 ) — sin ( x 0 2 ) = = sin 2 2 — sin 1 . 6 2 = sin 4 — sin 2 . 56 ≈ — 1 . 306

Так как приращение ∆ f ( x ) отрицательное из отрезка [ 1 . 6 ; 2 ] , то это указывает на убывание функции. Обозначим это графически.

Определение производной функции в точке

Когда функция вида f ( x ) определена из промежутка ( a ; b ) , тогда x 0 и x 0 + ∆ x считаются точками данного промежутка. Производная функции f ( x ) в точке x 0 — это предел отношений приращения функции к приращению аргумента, когда ∆ x → 0 . Данное определение записывается как f ‘ ( x 0 ) = lim ∆ x → 0 ∆ f ( x ) ∆ x .

Если последний предел принимает конкретное значение, тогда существует конечная производная в точке. Когда предел бесконечен, то и сама производная бесконечна в этой точке. Когда предел не существует, то и производной в заданной точке не существует.

Функция f ( x ) дифференцируема в точке x 0 , если конечная производная в ней существует.

Когда функция вида f ( x ) дифференцируема в каждой точке из промежутка ( a ; b ) , тогда функцию называют дифференцируемой на заданном промежутке. Отсюда получаем, что любая точка х из промежутка ( a ; b ) может принимать значения функции f ‘ ( x ) , иначе говоря, имеет место определение новой функции вида f ‘ ( x ) , которая называется производной функции f ( x ) из интервала ( a ; b ) .

Нахождение производной иначе называют дифференцированием

Из выше указанного получаем, что производная в точке является числом, а производная функции на промежутке является функцией. Когда необходимо вычислять производную, обязательно обращаемся к нахождению переделов.

Найти производную функции sin ( 2 x ) в точке x 0 = π 6 .

Решение

Для нахождения производной в точке необходимо начать с написания предела отношения приращения функции к приращению аргумента, применив тригонометрические формулы. Получаем, что

( sin ( 2 x 0 ) ) ‘ = lim ∆ x → 0 ∆ sin ( 2 x 0 ) ∆ x = lim ∆ x → 0 sin ( 2 ( x 0 + ∆ x ) ) — sin ( 2 x 0 ) ∆ x = = lim ∆ x → 0 2 · sin 2 ( x 0 + ∆ x ) — 2 x 0 3 · cos 2 ( x 0 + ∆ x ) + 2 x 0 2 ∆ x = = 2 · lim ∆ x → 0 sin ( ∆ x ) · cos ( 2 x 0 + ∆ x ) ∆ x

Для упрощения используем первый замечательный предел и в результате получаем, что

( sin ( 2 x 0 ) ) ‘ = 2 · lim ∆ x → 0 sin ( ∆ x ) · cos ( 2 x 0 + ∆ x ) ∆ x = = 2 · lim ∆ x → 0 sin ( ∆ x ) ∆ x · lim ∆ x → 0 cos ( 2 x 0 + ∆ x ) = = 2 · 1 · cos ( 2 x 0 + 0 ) = 2 cos ( 2 x 0 ) = 2 cos 2 · π 6 = = 2 cos π 3 = 2 · 1 2 = 1

Ответ: ( sin ( 2 x 0 ) ) ‘ = 1 .

Найти производную функции f ( x ) = 3 x 3 — 1 из промежутка x ∈ 1 3 3 ; + ∞

Решение

Для поиска производной из интервала понимаем, что результат должен быть функцией. Тогда x 0 = x , где значение х возьмем любое число из заданного промежутка x ∈ 1 3 3 ; + ∞ . Из определения видно, что производной считают отношение приращения функции на приращение аргумента, который стремится к нулю. Запишем

f ‘ ( x ) = 3 x 3 — 1 ‘ = lim ∆ x → 0 f ( x + ∆ x ) — f ( x ) ∆ x = = lim ∆ x → 0 3 ( 3 + ∆ x ) 3 — 1 — 3 x 3 — 1 ∆ x = » open=» 0 0

Получаем неопределенность в результате. Поэтому следует произвести домножение на сопряженное выражение для применения формул сокращенного умножения, приведения подобных слагаемых и последующим сокращением выражения. Тогда получим, что

f ‘ ( x ) = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 ∆ x = = lim ∆ x → 0 ( 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 ) ( 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 ) ∆ x · ( 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 ) = = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — 3 x 3 — 1 2 ∆ x · 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = lim ∆ x → 0 3 ( x + ∆ x ) 3 — 1 — ( 3 x 3 — 1 ) ∆ x · 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = 3 · lim ∆ x → 0 3 x 2 + 3 x ∆ x + ( ∆ x ) 2 3 ( x + ∆ x ) 3 — 1 + 3 x 3 — 1 = = 3 · 3 x 2 + 3 x · 0 + ( 0 ) 2 3 ( x + 0 ) 3 — 1 + 3 x 3 — 1 = 9 x 2 2 3 x 3 — 1

Ответ: 3 x 3 — 1 ‘ = 9 x 2 2 3 x 3 — 1 и x ∈ 1 3 3 ; + ∞

Для решения таких примеров необходимо учитывать то, что область определения функции f ( x ) может не совпадать с областью определения производной этой функции. Предыдущий пример имеет область определения вида D f x : x ∈ [ 1 3 3 ; + ∞ ) , а производная определена на интервале D f x : x ∈ 1 3 3 ; + ∞ . То есть при дифференцировании функция f ‘ ( x ) — это производная заданной функции f ( x ) из промежутка x ∈ D ( f ( x ) ) D ( f ‘ ( x ) ) .

Получение формул таблиц производных основано на определении производной. Они достаточно удобны, что способствует скорейшему дифференцированию сложных выражений. Использование понятия производной применяют для доказательств правил дифференцирования.

Дифференциальные и производные 2021

Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.

Функция является одной из основных концепций математики, которая определяет взаимосвязь между набором входов и множеством возможных выходов, где каждый вход связан с одним выходом. Одной переменной является независимая переменная, а другая переменная — зависимая переменная.

Концепция функции является одной из самых недооцененных тем в математике, но имеет важное значение для определения физических отношений. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.

В математике есть несколько исключений, или вы можете сказать о проблемах, которые не могут быть решены обычными методами геометрии и алгебры. Для решения этих проблем используется новая ветвь математики, известная как исчисление.

Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.

Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других отраслей математики. Дифференциал — это подполе исчисления, которое относится к бесконечно малой разности в некоторой переменной величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.

Что такое Дифференциал?

Дифференциал — одно из фундаментальных делений исчисления, а также интегральное исчисление. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой переменной величине. Мир, в котором мы живем, наполнен взаимосвязанными количествами, которые меняются периодически.

Например, площадь кругового тела, которая изменяется при изменении радиуса или снаряд, который изменяется со скоростью. Эти изменяющиеся сущности в математических терминах называются переменными, а скорость изменения одной переменной по отношению к другой является производной. И уравнение, представляющее связь между этими переменными, называется дифференциальным уравнением.

Дифференциальные уравнения — это уравнения, содержащие неизвестные функции и некоторые их производные.

Что такое производная?

Понятие производной функции является одним из самых мощных понятий в математике. Производной функции обычно является новая функция, которая называется производной функцией или функцией скорости.

Производная функции представляет собой мгновенную скорость изменения значения зависимой переменной по отношению к изменению значения независимой переменной. Это фундаментальный инструмент исчисления, который также можно интерпретировать как наклон касательной линии. Он измеряет, насколько крутой график функции находится в некоторой заданной точке графика.

Проще говоря, производная — это скорость, с которой функция изменяется в какой-то определенной точке.

Разница между дифференциальными и производными

Определение дифференциального Vs. производный

Оба термина дифференциальные и производные тесно связаны друг с другом с точки зрения взаимосвязи. В математике меняющиеся сущности называются переменными, а скорость изменения одной переменной по отношению к другой называется производной.

Уравнения, определяющие связь между этими переменными и их производными, называются дифференциальными уравнениями. Дифференциация — это процесс нахождения производной. Производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.

Связь дифференциальных Vs. производный

Дифференциация — это метод вычисления производной, которая является скоростью изменения выхода y функции относительно изменения переменной x.

Проще говоря, производная относится к скорости изменения y по х, и это соотношение выражается как y = f (x), что означает, что y является функцией x. Производные функции f (x) определяются как функция, значение которой порождает наклон f (x), где она определена, и f (x) дифференцируема. Это относится к наклону графика в данной точке.

Представление дифференциального Vs. производный

Дифференциалы представлены как dИкс, dу, dt и т. д., где dx представляет собой небольшое изменение x, dy представляет собой небольшое изменение y и dt — небольшое изменение t. При сравнении изменений связанных величин, где y — функция x, дифференциал dy может быть записана как:

dy = f ’ (Икс) dИкс

Производной функции является наклон функции в любой точке и записывается как d/dИкс. Например, производную от sin (x) можно записать в виде:

d/dx sin (x) = sin (x) ’ = cos (x)

Дифференциальная и производная: Сравнительная таблица

Резюме дифференциальных Vs. производный

В математике скорость изменения одной переменной по отношению к другой переменной называется производной, а уравнения, выражающие связь между этими переменными и их производными, называются дифференциальными уравнениями.В двух словах, дифференциальные уравнения включают производные, которые фактически определяют, как изменяется количество относительно другого. Решая дифференциальное уравнение, вы получаете формулу для количества, не содержащего производных. Метод вычисления производной называется дифференцированием. Проще говоря, производной функции является скорость изменения выходного значения по отношению к его входному значению, тогда как дифференциал — это фактическое изменение функции.