Путь и перемещение: что это и чем они отличаются?
Чем отличается перемещение от пути при движении тела?
Путь — это длина траектории движения материальной точки / тела / чего угодно.
Путь — скалярная величина, характеризуется только числом (ну и единицей измерения, естественно) .
Траектория — это слиния, по которой движется тело, иначе — совокупность всех точек — положений тела в любой момент времени.
Перемещение — это вектор, направленный из начального положения тела в конечное.
Перемещение — векторная величина.
Скалярной характеристикой является модуль перемещения — это расстояние между начальным и конечным положением тела. Если сравнивать модуль перемещения и путь, то разница существенная.
Так, на рисунке тело двигалось из точки А в точку В по некоторой кривой линии, на рисунке обозначенной красным цветом. Для любой точки этой линии найдётся момент времени, при котором тело побывало в этой точке и наоборот. Эта линия есть траектория. А длина этой линии есть путь, пройдённый телом или просто пройденный путь. Перемещение же есть вектор АВ, а модуль перемещения — расстояние по прямой линии между точками А и В (чёрная линия) . В некоторых точках чёрной линии движущееся тело вовсе не обязано быть.
Для того чтобы вычислить пройденный путь в общем случае нужно определить длину кривой, например, приближённо, путём разбиения её на большое число маленьких дуг, которые можно считать примерно прямыми отрезками.
Очевидно пройденный путь всегда не меньше перемещения, а точнее, модуля перемещения, т. е. либо больше его, либо равен ему, причём равен только тогда когда тело двигалось из точки А в точку В по кратчайшей траектории, т. е. по прямой. В этом и только в этом путь равен модулю перемещения.
Если пройденный путь равен нулю, то это значит, что тело в течение некоторого времени оставалось на месте и не двигалось. Перемещение в этом случае тоже равно нулю. Но если путь не равен нулю, то перемещение всё же может быть равно нулю (например, конец стрелки часов, сделав полный оборот, совершил путь по окружности, равный 2πR, где R где R — длина стрелки, а перемещение и модуль перемещения равны нулю — стрелка вернулась в исходное положение.
Ещё пример. Тело движется по двум сторонам треугольника. Тогда пройдённый путь равен сумме длин этих сторон, а модуль перемещения — длине третьей стороны. А сторона треугольника, даже самая длинная, всегда меньше суммы двух других сторон — здесь путь больше перемещения.
Часто возникает путаница с понятием средней скорости. Надо сразу иметь в виду, что скорость является вторичной характеристикой по отношению к пути, т. е не путь определяется как произведение скорости на время, а скорость по определению равна отношению пути ко времени. Так вот, средняя скорость — это отношение пути, пройденного телом ко времени за которое тело прошло этот путь. Если путь ненулевой, то и средняя скорость ненулевая. Вместо пути часто подставляют перемещение, что, вообще говоря, неправильно.
путь — это произведение скорости на время. а перемещение — это разность между конечными и начальными координатами
если проще, то путь всегда увеличивается, ты можешь делать два шага вперед, два назад, можешь кружок пройти, в любом случае, чем больше идешь, тем больше расстояние пройдешь,
при этом, перемещение может быть равным нулю (например, если ты прошел круг и остановился в начальной точке)
Я съездил из Санкт-Петербурга в Москву и обратно. Пройденный путь — 1300 км. Перемещение — ноль, я там же, где был. Теперь понятно?
А не наоборот? Путь — это длина движения, а перемещение — это разность координат
Путь — это длина траектории движения тела.
Перемещение — расстояние между начальной и конечной точками траектории. Примеры см. выше
а вот так сразу и не сформулируешь,
Путь это как бы общая полезность движения, а перемещение это просто перемещение
Иными словами если ты будешь петлять по кругу путь будет маленький, а перемещение постоянно расти
Катался на детской карусели с лошадками? А далеко уехал? Вот тебе и ответ !
«Перемещение. Траектория. Путь» (9-й класс)
Разделы: Физика
Класс: 9
- Образовательная:
– ввести понятия “перемещение”, “путь”, “траектория”. - Развивающая:
– развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию. - Воспитательная:
– достигать высокой активности класса, внимания, сосредоточенности учащихся.
-
пластмассовая бутылка вместимостью 0,33 л с водой и со шкалой;
- медицинский флакончик вместимостью 10 мл (или малая пробирка) со шкалой.
Демонстрации: Определение перемещения и пройденного пути.
1. Актуализация знаний.
– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями (терминами), касающихся этой темы. А пока проверим выполнение вами домашнего задания у данному уроку.
2. Проверка домашнего задания.
Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:
Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника. [1]
1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:
а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.
2. Дано выражение: S = υ0 · t + (а · t 2 ) / 2, выразите: а, υ0
1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:
а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.
2. Дано выражение: S = (υ 2 – υ 0 2 ) / 2 · а, выразите: υ 2 , υ 0 2 .
3. Изучение нового теоретического материала.
С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой 
. В СИ перемещение измеряется в метрах (м).
[ ] – [ м ] – метр.
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.
– вектор, проведенный из точки М в М1
Знать вектор перемещения – значит, знать его направление и модуль. Модуль вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор перемещения тела, можно определить, где находится тело.
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.
Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Длина траектории – это ПУТЬ. Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3) (раздаются в виде карточек каждому ученику)
- Путь – скалярная величина и характеризуется только числовым значением.
- Перемещение – векторная величина и характеризуется как числовым значением (модулем), так и направлением.
- При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
- Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
| Путь | Перемещение | |
| Определение | Длина траектории, описываемой телом за определенное время | Вектор, соединяющий начальное положение тела с его последующим положением |
| Обозначение | l [ м ] | S [м ] |
| Характер физических величин | Скалярная, т.е. определяется только числовым значением | Векторная, т.е. определяется числовым значением (модулем) и направлением |
| Необходимость введения | Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t | Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t |
| l = S в случае прямолинейного движения без возвратов | ||
4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)
- Заполните водой до горловины пластмассовую бутылку со шкалой.
- Флакончик со шкалой заполните водой на 1/5 его объема.
- Наклоните бутылку так, чтобы вода подошла к горловине, но не вытекала из бутылки.
- Быстро опустите флакончик с водой в бутылку (не закрывая его пробкой) так, чтобы горловина флакончика вошла в воду бутылки. Флакончик плавает на поверхности воды в бутылке. Часть воды при этом из бутылки выльется
- Завинтите крышку бутылки.
- Сжимая боковые стенки бутылки, опустите поплавок на дно бутылки.
- Ослабляя давление на стенки бутылки, добейтесь всплытия поплавка. Определите путь и перемещение поплавка:________________________________________________________
- Опустите поплавок на дно бутылки. Определите путь и перемещение поплавка:______________________________________________________________________________
- Заставьте поплавок всплыть и утонуть. Каков путь и перемещение поплавка в этом случае?_______________________________________________________________________________________
5. Упражнения и вопросы для повторения.
- Путь или перемещение мы оплачиваем при поездке в такси? (Путь)
- Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. найти путь и перемещение мяча. (Путь – 4 м, перемещение – 2 м.)
Повторение понятий урока:
– перемещение;
– траектория;
– путь.
7. Домашнее задание.
§ 2 учебника [1], вопросы после параграфа, упражнение 2 (стр.12) учебника [1], повторить выполнение опыта урока дома.
1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.
Путь и перемещение тела
С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.
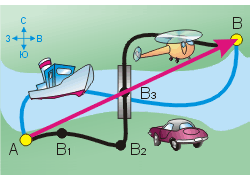
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.
Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.
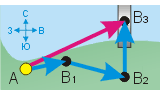
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.
Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом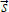 
(важно: со стрелочкой). Символом s без стрелочки обозначают модуль перемещения. Примечание: изображение любого вектора на чертеже (в виде стрелки) или упоминание его в тексте (в виде слова) делает необязательным наличие стрелочки над обозначением.
Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.
Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
Решение 1 – с измерениями линейкой и транспортиром.
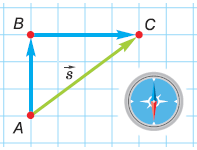
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).
Решение 2 – без использования линейки и транспортира.
Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:
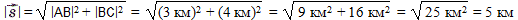
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
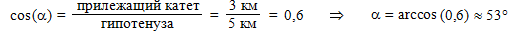
Итак, задача решена двумя способами с совпадающими ответами.
Путь и перемещение
При своем движении материальная точка описывает некоторую линию, которую называют ее траекторией движения. Траектория может быть прямой линией, а может представлять собой кривую.
Путь — длина участка траектории, который прошла материальная точка за рассматриваемый отрезок времени. Путь — это скалярная величина.
При прямолинейном движении в одном направлении пройденный путь ($Delta s$) равен модулю изменения координаты тела. Так, если тело двигалось по оси X, то путь можно найти как:
где $x_1$ — координата начального положения тела; $x_2$ — конечная координата тела.
Его можно вычислить, если известен модуль скорости ($v=v_x$):
[Delta s=vt left(2right),]
где $t$ — время движения тела.
Графиком, который отображает зависимость пути от времени при равномерном прямолинейном движении, является прямая (рис.1). С увеличением величины скорости увеличивается угол наклона прямой относительно оси времени.
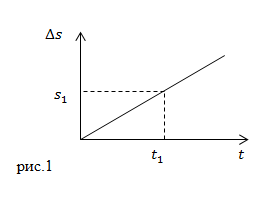
Если по графику $Delta s(t)$ необходимо найти путь, который проделало тело за время $t_1$, то из точки $t_1$ на оси времени проводят перпендикуляр до пересечения с графиком $Delta s(t)$. Затем из точки пересечения восстанавливают перпендикуляр к оси $Delta s$. На пересечении оси и перпендикуляра получают точку $
Путь не бывает меньше нуля и не может уменьшаться при движении тела.
Перемещение
Перемещением называют вектор, который проводят из начального положения движущейся материальной точки в ее конечное положение:
[Delta overline
Вектор перемещения численно равен расстоянию между конечной и начальной точками и направлен от начальной точки к конечной.
Приращение радиус-вектора материальной точки — это перемещение ($Delta overline
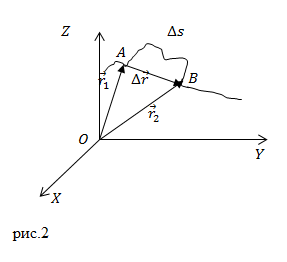
В декартовой системе координат радиус-вектор точки представляют в виде:
[overline
где $overline$, $overline
[Delta overline
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и длина вектора перемещения равна пройденному точкой пути:
[left|Delta overline
Длину вектора перемещения (как и любого вектора) можно обозначать как $left|Delta overline
Если тело совершает несколько перемещений, то их можно складывать по правилам сложения векторов:
Если направление движения тела изменяется, то модуль вектора перемещения не равен пройденному телом пути.
Примеры задач на путь и перемещение
Задание: Мяч бросили вертикально вверх от поверхности Земли. Он долетел до высоты 20 м. и упал на Землю. Чему равен путь, который прошел мяч, каков модуль перемещения?
Решение: Сделаем рисунок.
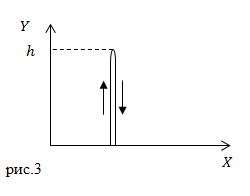
В нашей задаче мяч движется прямолинейно сначала вверх, затем вниз. Так как путь — длина траектории, то получается, что мяч дважды прошел расстояние h, следовательно:
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю:
Ответ: $ Путь Delta s=2h$. Перемещение $Delta r=0$
Задание: В начальный момент времени тело находилось в точке с координатами $(x_0=3;; y_0=1)$(см). Через некоторый промежуток времени оно переместилось в точку координаты которой ($x=2;;y=4$) (см). Каковы проекции вектора перемещения на оси X и Y?
Решение: Сделаем рисунок.
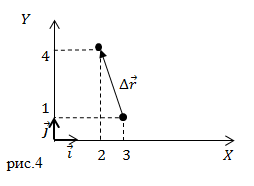
Радиус — вектор начальной точки запишем как:
[
Радиус — вектор конечной точки имеет вид:
[overline
Вектор перемещения представим как:
[Delta overline
Из формулы видим, что:
[Delta r_x=-1;;Delta r_y=3. ]
Ответ: $Delta r_x=-1;;Delta r_y=3 $
Путь и перемещение: что это и чем они отличаются?
Ежеминутно сквозь человека проходит 1 000 000 000 000 000 элементарных частиц — нейтрино. Однако это не вредит человеческому здоровью. Нейтрино могут проникать через любые предметы, не взаимодействуя с ними.
—>СТАТИСТИКА —>
—>МЫ ВКОНТАКТЕ —>
—>НЕМНОГО РЕКЛАМЫ —>
Наши спонсоры
- Уроки Photoshop
- Онлайн ТВ
Чтобы разобраться с такими понятиями как траектория, путь и перемещение рассмотрим пример.
Представим человечка, который гуляет по лабиринту. Он может ходить по этому лабиринту хоть целый день и пройти десятки километров: поворачивать то направо, то налево, то возвращаться и проходить по одним и тем же дорожкам снова и снова, пока не найдет выход.
Мы же, как самые хитрые, наблюдаем за его попытками выйти из лабиринта сверху, и нам он кажется маленькой точкой в лабиринте.
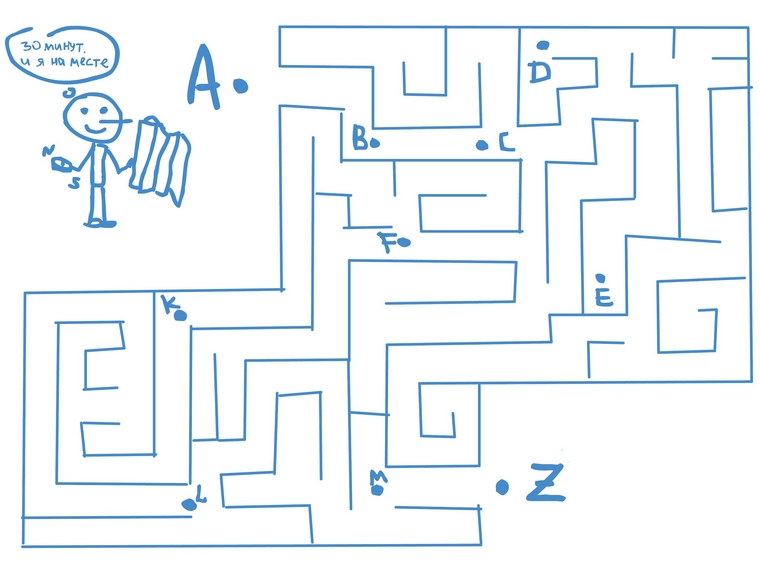
Синие точки – это положение нашего человечка в лабиринте в разное время.
Если бы человечек чертил за собой линию, то мы могли бы увидеть весь его маршрут за день – получилась бы сложная линия с изгибами и петлями. По-умному эта линия называется траекторией.
Человечек не захотел чертить за собой линию и поручил это дело помощнику.
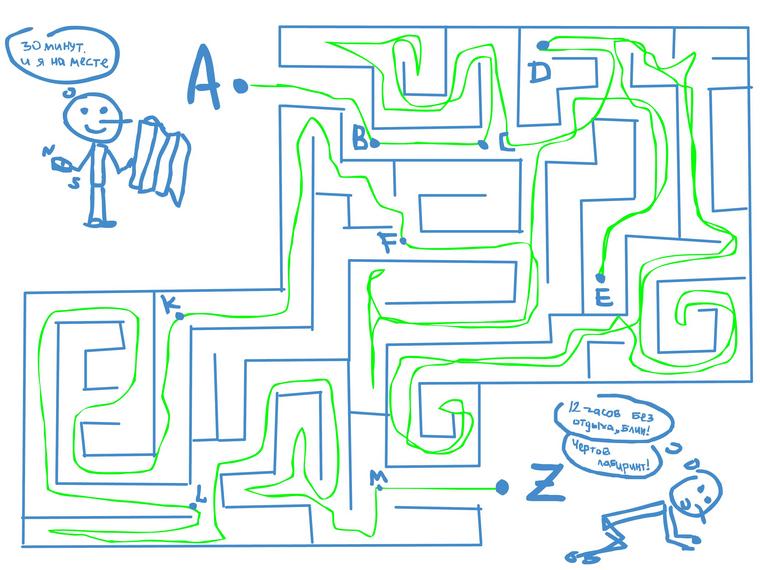
На рисунке зеленой линией указана траектория движения человечка
Траектория — это линия, которую описывает тело при своем движении.
Траектория бывает двух видов: в виде прямой линии ( прямолинейной ) и в виде кривой линии ( криволинейной ).
На рисунке траектория на участках BC и MZ прямолинейная, а на участках AB, CD, DE, EF, FK, KL, LM – криволинейная.
Если мы измерим длину всей зеленой линии ABCDEFKLMZ (траектории), то получим путь. Путь — длина траектории.
Вроде все просто, если бы не одно НО. Кроме пути физики еще придумали такое понятие как перемещение. Чем же путь отличается от перемещения? Разве это не одно и то же?!
Перемещение – это, если мы не будем следить за траекторией движения человечка весь день, а просто отметим точку на карте в начале его движения (Точка А) и затем в конце дня отметим точку, где он закончил свое движение (Точка Z), и потом просто соединим эти две точки прямой линией. Длина этой прямой линии и будет перемещение человечка за день.
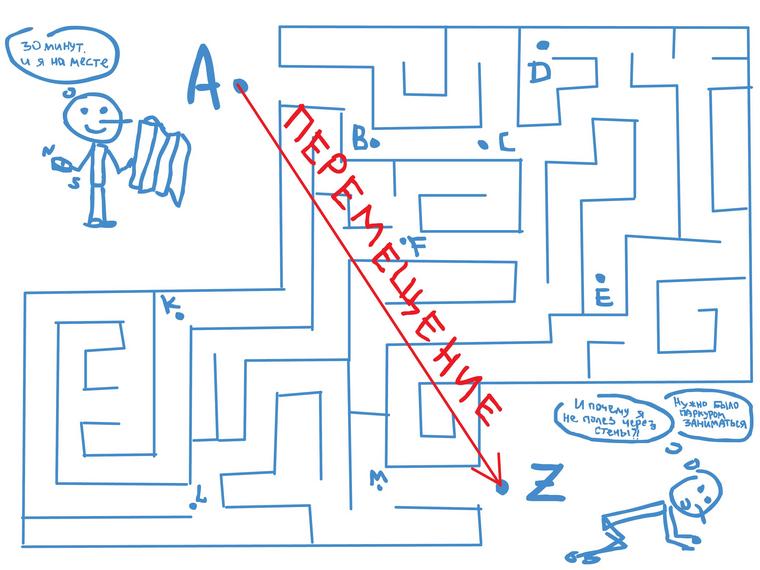
Перемещение человечка – направленный красный отрезок AZ
Соединять начальную и конечную точку принято стрелочкой, которая указывает направление, в котором переместилось тело. Таким образом, перемещение – это длина прямой стрелочки (направленного отрезка), соединяющей начальное и конечное положение тела.
ВЫВОДЫ:
Траектория — воображаемая линия, по которой движется тело.
Путь — длина траектории.
Перемещение — направленный отрезок, соединяющий начальное и конечное положения тела.
P.S. Путь и перемещение равны, если тело двигается всегда по прямой. Перемещение тела может быть равно нулю, а путь одновременно равен десяткам и тысячам километров (если тело вернется в ту же точку, откуда и начало двигаться).
Как видите путь и перемещение — это разные вещи.
