В чем разница между натуральными и целыми числами?
В чем разница между натуральными и целыми числами?

Определяющее понятие математики – число, которое используется для количественной характеристики объектов. Наука оперирует их несколькими видами. Осознание особенностей этого понятия поможет избежать ошибок, приблизит открытие новых горизонтов познания точной науки.
Считать человек научился тогда, когда научился говорить. Первоначально это было определение количества предметов, товара. При появлении письменности придумали специальные значки – цифры. В этой стать речь пойдёт о натуральных и целых числах, как самых простых.
Натуральные числа
На заре цивилизации первобытные люди обходились понятиями «один» и «много». Древние охотники не утруждали себя подсчётами. При возникновении товарообменных отношений назрела потребность усложнить счёт.
Во время торговли приходилось считать количество товара. Тогда появились самые простые числа. Их называют натуральными, так как возникли естественным образом при счёте. Ими описывают количество предметов или порядковый номер ряда подобных объектов. Для письменного отображения этих величин используют специальные знаки, которые называют цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Пример записи: двести тридцать один – 231.
Самая маленькая величина – единица (1), самой большой нет. Если возьмём самое большое, на наш взгляд, значение, к нему всегда можно добавить ещё 1, получить большее, и так до бесконечности.
При их расположении последовательно в порядке возрастания получаем числовой ряд. Каждый следующий элемент ряда увеличивается на 1 по отношению к предыдущему. Этот массив элементов обозначают N= . Сюда не входит ноль, он применяется только для описания многозначных величин.
Если выражение содержит только один значок, то оно называется однозначным. Например: 1, 3, 7. Если запись имеет больше одной цифры, то она многозначная. К примеру, числа: 15, 23, 78 – двузначные, 125, 561, 938 – трёхзначные, 2589, 1596, 3564 – четырёхзначные. Математика использует десятичную систему исчисления. При записи каждому значку соответствует своё определённое значение в зависимости от расположения. Например, 286:
- Последняя шесть означает 6 единиц.
- Предпоследняя восемь – 8десятков.
- Первая двойка – 2 сотни.
В этой записи две сотни, восемь десятков и шесть единиц.
Целые числа
У этого понятия определение шире. Сюда входят элементы, описанные выше, а также противоположные по значению и 0. В итоге, имеем бесконечное количество натуральных (1, 2, 3, 4, …) и столько же противоположных значений.
Совокупность их с нолём называется целыми.Они бывают положительными и отрицательными. Первые подразумевают знак плюс (обычно не пишется). Примеры таких записей: 8, 15, 127, 3259.
Отрицательные целые имеют знак минус (всегда пишется): −9, −21, −832, −4785. Они появились при развитии товарообменных отношений. Так было удобно считать долги. Например, торговцу заплатили за мешок вяленой рыбы одну шкурку лисы, а надо было три, то долг составит ещё две шкурки: 1− 3 = −2.
Ноль стоит обособленно. Он не принадлежит ни к тем, ни к другим. Все что больше него – положительные, меньше – отрицательные. Множество этих элементов обозначают Z= . С ними выполняют основные математические действия, нельзя только делить на ноль. Этими значениями принято описывать количественное изменение предметов или физических явлений во времени.
Общие черты понятий
- Оба выполняют количественную характеристику предметов или каких-то параметров.
- Натуральные значения входят во множество целых, то есть любое из них будет целым.
- Математические действия кроме деления и извлечения корня с обоими видами даёт целое.
- Самого большого числа для них нет – исчезает в бесконечности.

Отличия чисел
Наряду с общими признаками у этих понятий есть различия в написании, значениях и функциях.
Натуральные всегда больше ноля, целые – положительные, отрицательные и 0, поэтому не каждое целое будет натуральным.
У первых самое маленькое значение единица, у вторых его нет, оно бесконечно малое. Какую бы маленькую величину мы не придумали, от неё всегда можно отнять единицу и получить ещё меньшую и так бесконечно много раз.
Целыми легче описывать изменение количества, чем натуральными. При этом нет необходимости конкретно указывать увеличение или уменьшение численности. Само число характеризует эту перемену, а знак перед ним указывает направление. Вот примеры такого описания. Пусть в библиотеке есть некоторое количество книг. Если туда привезут еще восемьдесят, то их станет больше, а 80 выражает это изменение перечня в сторону повышения. Если же из библиотеки заберут тридцать книг, то их станет меньше, а 30 будет выражать перемену в сторону снижения. В библиотеку не будут привозить и увозить издания, то говорят о неизменности наличия литературы, то есть произошла нулевая перемена.
Этот пример показывает преобразование объёма книг с помощью целых чисел 80, −30 и 0 соответственно. Положительное 80 передаёт рост численности, отрицательное −30 выражает её понижение (отрицательная величина). Ноль показывает, что сумма предметов осталось без изменения.
Целыми хорошо описывается варьирование физических величин. При увеличении температуры на 3 градуса, это указывается значением 3. Уменьшение температуры на 10 градусов записывается как число с минусом: −10. А постоянство температуры определяется нолём.
Не каждый из нас математик, но понимание основ этой науки сыграет позитивную роль для каждого. Элементарные математические знания не раз выручат в трудной ситуации.
Алгебра
План урока:
Натуральные числа
Ещё в далекие доисторические времена человек освоил такую математическую операцию, как счет. Можно было подсчитать количество соплеменников в племени или животных в стае, на которых велась охота. При этом человек ещё не осознавал понятие числа как некое отвлеченное понятие. Анализ языков народов, находящихся на самых низких стадиях развития, показывает, что они в словосочетаниях «три змеи», «три палки», «три камня» используют разные слова для числа 3. Однако со временем человек осознал, что количество предметов можно определять числом, которое не будет зависеть от природы подсчитываемых объектов. Числа, используемые для счета, сегодня называют натуральными числами. Долгое время человечество не знало никаких других чисел.


В качестве примера можно привести следующие натуральные числа: 1, 8, 10, 1000, 64141 и т.п. Если можно представить, что в каком-то множестве содержится N элементов, то N будет натуральным числом.
Вообще все натуральные числа являются частью так называемого натурального ряда чисел. Начинается этот ряд с единицы, а каждое следующее число больше предыдущего на 1.

Таким образом, можно дать ещё одно определение натуральных чисел – это числа, входящие в натуральный ряд. Традиционно ноль не является натуральным числом, ведь при подсчете предметов счет начинают с единицы. Такой подход используется в большинстве российских источников. Однако стоит отметить, что иногда в зарубежной литературе всё же предпочитают начинать натуральный ряд не с единицы, а с нуля. В этом случае 0 становится натуральным числом. Это деление весьма условно. Для обозначения множества натуральных чисел используется буква N. Очевидно, что натуральных чисел существует бесконечно много, а потому не существует наибольшего натурального числа.
Любые два натуральных числа можно складывать друг с другом и перемножать, при этом в результате будет снова получаться натуральное число. При вычитании может получиться ноль или отрицательное число, а при делении – дробное.
Простые и составные числа
Все натуральные числа можно разбить на три группы:
- простые числа;
- единица;
- составные числа.

Единицу традиционно не считают ни простым, ни составным числом. Составным же называют натуральное число, делящееся не только на единицу и себя. Можно дать и другие определения, основанные на количестве делителей у числа. Так, единица имеет ровно 1 делитель. У простого числа всегда ровно 2 делителя, а у составного – 3 и более.
В качестве примера простых чисел можно привести: 2, 3, 5, 7, 31, 101, 163. Примерами составных чисел являются:
- 4 (делится на 2);
- 6 (делится на 2 и 3);
- 8 (делится на 2 и 4);
- 33 (делится на 3 и 11)
- 50 (делится на 2, 5, 10, 25).
Среди делителей составного числа могут быть как другие составные, так и простые числа. Например, 50 имеет простые делители 2 и 5 и составные 10 и 25.
Заметим, что если число n делится на m, а m в свою очередь делится на k, то и n делится на k. Так, 45 делится на 9, а 9 делится на 3. Значит, и 45 делится на 3. Из этого свойства чисел вытекает следующее утверждение:
Любое составное число имеет хотя бы один простой делитель, причем им обязательно будет наименьший из всех делителей числа. Докажем это. Пусть число H – составное, и имеет наименьший делитель F. Предположим, что F – составное число. Тогда у него есть делитель L, который меньше его. Но тогда L должен быть делителем и для H. Так как L 1 1
Целые числа: общее представление
В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.
Целые числа. Определение, примеры
Вначале вспомним про натуральные числа ℕ . Само название говорит о том, что это такие числа, которые естественно использовались для счета с незапамятных времен. Для того, чтобы охватить понятие целых чисел, нам нужно расширить определение натуральных чисел.
Определение 1. Целые числа
Целые числа — это натуральные числа, числа, противоположные им, и число нуль.
Множество целых чисел обозначается буквой ℤ .
Множество натуральных чисел ℕ — подмножество целых чисел ℤ . Любое натуральное число является целым, но не любое целое число является натуральным.
Из определения следует, что целым является любое из чисел 1 , 2 , 3 . . , число 0 , а также числа — 1 , — 2 , — 3 , . .
В соответствии с этим, приведем примеры. Числа 39 , — 589 , 10000000 , — 1596 , 0 являются целыми числами.
Целые числа и координатная прямая
Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.
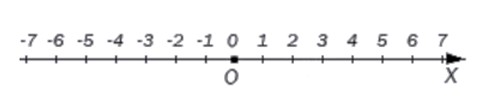
Началу отсчета на координатной прямой соответствует число 0 , а точкам, лежащим по обе стороны от нуля соответствуют положительные и отрицательные целые числа. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.
Положительные и отрицательные целые числа
Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.
Определение 2. Положительные целые числа
Положительные целые числа — это целые числа со знаком «плюс».
Например, число 7 — целое число со знаком плюс, то есть положительное целое число. На координатной прямой это число лежит справа от точки отсчета, за которую принято число 0 . Другие примеры положительных целых чисел: 12 , 502 , 42 , 33 , 100500 .
Определение 3. Отрицательные целые числа
Отрицательные целые числа — это целые числа со знаком «минус».
Примеры целых отрицательных чисел: — 528 , — 2568 , — 1 .
Число 0 разделяет положительные и отрицательные целые числа и само не является ни положительным, ни отрицательным.
Любое число, противоположное положительному целому числу, в силу определения, является отрицательным целым числом. Справедливо и обратное. Число, обратное любому отрицательному целому числу, есть положительное целое число.
Можно дать другие формулировки определений отрицательных и положительных целых чисел, используя их сравнение с нулем.
Определение 4. Положительные целые числа
Положительные целые числа — это целые числа, которые больше нуля.
Отрицательные целые числа — это целые числа, которые меньше нуля.
Соответственно, положительные числа лежат правее начала отсчета на координатной прямой, а отрицательные целые числа находятся левее от нуля.
Ранее мы уже говорили, что натуральные числа — это подмножество целых. Уточним этот момент. Множество натуральных чисел составляют целые положительные числа. В свою очередь, множество отрицательных целых чисел является множеством чисел, противоположных натуральным.
Любое натуральное число можно назвать целым, но любое целое число нельзя назвать натуральным. Отвечая на вопрос, являются ли являются ли отрицательные числа натуральными, нужно смело говорить — нет, не являются.
Неположительные и неотрицательные целые числа
Определение 6. Неотрицательные целые числа
Неотрицательные целые числа — это положительные целые числа и число нуль.
Неположительные целые числа — это отрицательные целые числа и число нуль.
Как видим, число нуль не является ни положительным, ни отрицательным.
Примеры неотрицательных целых чисел: 52 , 128 , 0 .
Примеры неположительных целых чисел: — 52 , — 128 , 0 .
Неотрицательное число — это число, большее или равное нулю. Соответственно, неположительное целое число — это число, меньшее или равное нулю.
Термины «неположительное число» и «неотрицательное число» используются для краткости. Например, вместо того, чтобы говорить, что число a — целое число, которое больше или равно нулю, можно сказать: a — целое неотрицательное число.
Использование целых чисел при описании изменения величин
Для чего используются целые числа? В первую очередь, с их помощью удобно описывать и определять изменение количества каких-либо предметов. Приведем пример.
Пусть на складе хранится какое-то количество коленвалов. Если на склад привезут еще 500 коленвалов, то их количество увеличится. Число 500 как раз и выражает изменение (увеличение) количества деталей. Если потом со склада увезут 200 деталей, то это число также будет характеризовать изменение количества коленвалов. На этот раз, в сторону уменьшения.
Если же со склада ничего не будут забирать, и ничего не будут привозить, то число 0 укажет на неизменность количества деталей.
Очевидное удобство использования целых чисел в отличие от натуральных в том, что их знак явно указывает на направление изменения величины (увеличение или убывание).
Понижение температуры на 30 градусов можно охарактеризовать отрицательным числом — 30 , а увеличение на 2 градуса — положительным целым числом 2 .
Приведем еще один пример с использованием целых чисел. На этот раз, представим, что мы должны отдать кому-то 5 монет. Тогда, можно сказать, что мы обладаем — 5 монетами. Число 5 описывает размер долга, а знак «минус» говорит о том, что мы должны отдать монеты.
Если мы должны 2 монеты одному человеку, а 3 — другому, то общий долг ( 5 монет) можно вычислить по правилу сложения отрицательных чисел:
Что такое целые числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о ЦЕЛЫХ ЧИСЛАХ.
Это весьма обширное понятие из математики, с которым школьники сталкиваются уже в 5 классе.

Целые числа — это.
Целые числа – это все положительные, все отрицательные числа и ноль. Главное, чтобы они не содержали дробной части.
Согласно этому определению, к целым числам можно отнести:
-1256, -35, -9, 0, 14, 95, 2020
и так далее. Ведь у них нет дробной части. А вот числа:
0.5, 13.1319, ½, -¾, — 237.3
и так далее не могут считаться целыми, так как у них есть какие-то цифры после запятой или они являются дробью.
Все многообразие целых чисел называется множеством целых чисел. Это официальный математический термин. И обозначается он буквой Z.
В это множество входят и так называемые натуральные числа (это что?). Это все те, которые имеют положительное значение, но опять же без дробной части. Проще говоря, все числа, которые мы используем при счете. Например, 1, 2, 5, 10, 100 и так далее.
Множество натуральных чисел обознается буквой N. И зависимость его и множества целых чисел наглядно показана на следующем рисунке.
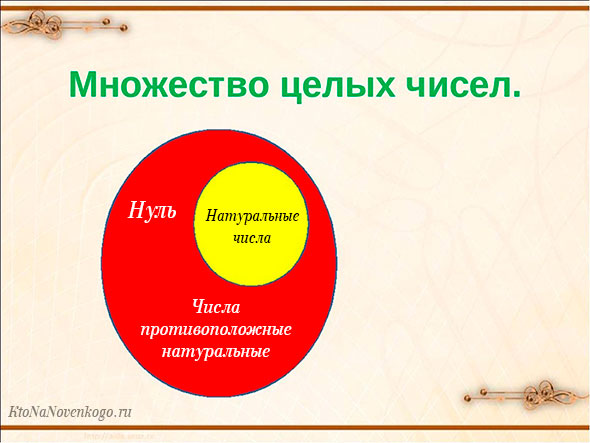
Отсюда можно сделать важный вывод:
Любое натуральное число автоматически является еще и целым. Но при этом далеко не каждое целое число является еще и натуральным.
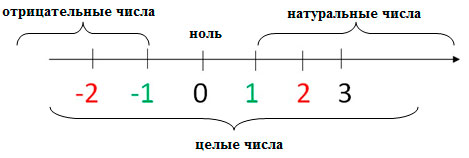
А можно представить это и в таком варианте. Целые числа — это:
- Натуральные числа;
- Ноль;
- Отрицательные числа.
Каким бы определением вы не пользовались, главное, чтобы было все понятно.
История изучения целых чисел
Опять же эту историю нужно разделить на три части. Ведь изучение натуральных чисел, а также открытие нуля и отрицательных чисел происходило независимо друг от друга. Да еще и в разных странах.
Изучение натуральных чисел
Тут все максимально просто. Эти числа возникли, как только человеку понадобилось считать – будь то куски мяса или количество бревен для дома.
Более точное изучение натуральных чисел начинается в Древнем Египте и Древней Месопотамии, а это более 6 тысяч лет назад.
А современные математики опираются на то, что после себя оставил древнегреческий ученый Пифагор. Он как раз активно собирал египетские и вавилонские данные, а после отразил их в своих трудах.
Открытие нуля
Конечно, египтяне, вавилоняне и даже греки знали о существовании нуля. Но не считали его числом, а потому не пользовались им. Это, кстати, приносило им немало сложностей. Они порой часами решали задачки, которые нынешний школьник посчитает за минуту.
Но официально число ноль появилось в 5-м веке. И «изобрели» его в Индии. Дело в том, что у местных жителей всегда существовало убеждение, что «ничто – это тоже что-то». Даже понятие Нирвана, которое обозначает состояние небытие, зародилось именно в Индии.
Потому-то там и придумали символ, который обозначал бы «ничто». Авторами его стали математики Брахмагупта и Ариабхата.

Как видите, индийский символ нуля очень похож на современный. Ну, разве что приплюснут и больше напоминает правильную окружность. Форма выбрана не случайно. По индийским поверьям, ноль символизирует круговорот жизни и мироздания. Его еще называют «змея вечности».
Когда арабы завоевали часть Индии, они переняли все математические знания. А во время крестовых походов многое, в том числе и цифры, перекочевали в Европу. Хотя потребовалось еще несколько сотен лет, чтобы «ноль» стал неотъемлемой частью европейской науки.
Открытие отрицательных чисел
Отрицательные числа первыми начали изучать китайцы во 2 веке до нашей эры. Их использовали в торговле и называли «долгами». А обычные числа – «имуществом». А для записи отрицательных чисел использовали перевернутый вид.

А вот в Европе к ним очень долго относились пренебрежительно, считая «несуществующими» и «абсурдными». Лишь в 12 веке математик Леонардо Фибоначчи (автор знаменитого числового ряда) описал их в своей книге «Книга Абака».
В середине 16 века математик Михаил Штифель посвятил им целый раздел в своей книге «Полная арифметика».
Но признание они получили лишь в 17 веке, после того как известный Рене Декарт создал свою систему координат.

В ней он также использовал нуль, привязав к нему положительные и отрицательные числа. Одни находились справа от него, а другие – слева.
Свойства целых чисел
Всем целым числам свойственны следующие характеристики:
-
Замкнутость. При математических действиях с целыми числами, за исключением деления, получаются только целые числа.
Если А и В – целые, то А+В=целое, А-В=целое и А*В=целое
Ассоциативность. При сложении или умножении трех и более целых чисел их можно менять местами, и результат не изменится.
(А + В) + С = А + (В + С)
Коммутативность. При перестановке мест слагаемых (множителей) – сумма (произведение) не меняется.
А + В = В + А, А * В = В * А
Если ноль участвует в сложении или вычитании, то значение остается неизменным.
А + 0 = 0, А – 0 = 0
Противоположность. При сложении одинаковых чисел с разными знаками, получается всегда ноль.
Разность знаков. При умножении чисел с разными знаками, результат всегда отрицательный. Если знаки одинаковые, то результат всегда положительный.
А * А = АА, А * (-А) = -АА, (-А) * (-А) = АА

Добавим: точно такое же правило действует и при делении. Минус на минус дают плюс. А минус на плюс или плюс на минус всегда дают минус.
Вместо заключения
Мы уже рассказали, с каким трудом в нашу жизнь попали отрицательные числа. Но сегодня они широко используются не только в математике.
- География. Высоту гор измеряют положительными значениями, а вот глубину водоемов – отрицательными. А уровень моря является нулем.
- История. Понятие «наша эра» разделила историю на положительное летоисчисление и отрицательное. Все, что происходило, более 2 тысяч лет назад можно описать как «в минус 125 году» или «в -3000 лет». Хотя больше принято говорить «125 год до н.э» и «3000 лет до н.э.».
- Медицина. Для определения остроты зрения врачи используют понятия отрицательных и положительных диоптрий. Идеальное зрение – это ноль. Минус – близорукость (не видит вдалеке), а плюс – дальнозоркость (не видит вблизи).
- Физика. Есть такие понятия, как положительно и отрицательно заряженные частицы. Одни называются протонами, а другие – электронами.
Ну и, наконец, слова положительный и отрицательный используются и в более разговорном смысле, как синонимы хорошего и плохого.
Например, в книгах и фильмах обязательно есть положительные и отрицательные герои. Также и наши черты характера, эмоции и поступки можно разделить на эти две категории.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Сами по себе числа ничего не значат, будь они даже целыми и натуральными, чтобы в них был смысл, они должны иметь привязку к чему-либо. Например, единица меньше пятидесяти, но всегда ли единица меньше? Если я скажу, что один рубль меньше пятидесяти копеек, то это будет ложью.
В чем разница между натуральными и целыми числами?

Определяющее понятие математики — число, которое используется для количественной характеристики объектов. Наука оперирует их несколькими видами. Осознание особенностей этого понятия поможет избежать ошибок, приблизит открытие новых горизонтов познания точной науки.
Считать человек научился тогда, когда научился говорить. Первоначально это было определение количества предметов, товара. При появлении письменности придумали специальные значки — цифры. В этой стать речь пойдёт о натуральных и целых числах, как самых простых.
- Натуральные числа
- Целые числа
- Общие черты понятий
- Отличия чисел
- Натуральные и целые числа
- Какие числа называются целыми
- Определение целых чисел
- Свойства целых чисел
- Положительные и отрицательные целые числа
- Неположительные и неотрицательные целые числа
- Целых числа в описании изменения величины
Натуральные числа
На заре цивилизации первобытные люди обходились понятиями «один» и «много». Древние охотники не утруждали себя подсчётами. При возникновении товарообменных отношений назрела потребность усложнить счёт.
Во время торговли приходилось считать количество товара. Тогда появились самые простые числа. Их называют натуральными, так как возникли естественным образом при счёте. Ими описывают количество предметов или порядковый номер ряда подобных объектов. Для письменного отображения этих величин используют специальные знаки, которые называют цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Пример записи: двести тридцать один — 231.
Самая маленькая величина — единица (1), самой большой нет. Если возьмём самое большое, на наш взгляд, значение, к нему всегда можно добавить ещё 1, получить большее, и так до бесконечности.
При их расположении последовательно в порядке возрастания получаем числовой ряд. Каждый следующий элемент ряда увеличивается на 1 по отношению к предыдущему. Этот массив элементов обозначают N=<1, 2, 3, …n, …>. Сюда не входит ноль, он применяется только для описания многозначных величин.
Если выражение содержит только один значок, то оно называется однозначным. Например: 1, 3, 7. Если запись имеет больше одной цифры, то она многозначная. К примеру, числа: 15, 23, 78 — двузначные, 125, 561, 938 — трёхзначные, 2589, 1596, 3564 — четырёхзначные. Математика использует десятичную систему исчисления. При записи каждому значку соответствует своё определённое значение в зависимости от расположения. Например, 286:
- Последняя шесть означает 6 единиц.
- Предпоследняя восемь — 8десятков.
- Первая двойка — 2 сотни.
В этой записи две сотни, восемь десятков и шесть единиц.
С ними производят математические действия: сложение, вычитание, умножение, деление, а также возведение в степень и извлечение корня. Но только при умножении и сложении получают натуральные числа. Если выполнять другие действия, то получим целую или дробную величину.
Целые числа
У этого понятия определение шире. Сюда входят элементы, описанные выше, а также противоположные по значению и 0. В итоге, имеем бесконечное количество натуральных (1, 2, 3, 4, …) и столько же противоположных значений.
Совокупность их с нолём называется целыми.Они бывают положительными и отрицательными. Первые подразумевают знак плюс (обычно не пишется). Примеры таких записей: 8, 15, 127, 3259.
Отрицательные целые имеют знак минус (всегда пишется): −9, −21, −832, −4785. Они появились при развитии товарообменных отношений. Так было удобно считать долги. Например, торговцу заплатили за мешок вяленой рыбы одну шкурку лисы, а надо было три, то долг составит ещё две шкурки: 1− 3 = −2.
Ноль стоит обособленно. Он не принадлежит ни к тем, ни к другим. Все что больше него — положительные, меньше — отрицательные. Множество этих элементов обозначают Z=<… −3, −2, −1, 0, 1, 2, 3, …>. С ними выполняют основные математические действия, нельзя только делить на ноль. Этими значениями принято описывать количественное изменение предметов или физических явлений во времени.
Общие черты понятий
- Оба выполняют количественную характеристику предметов или каких-то параметров.
- Натуральные значения входят во множество целых, то есть любое из них будет целым.
- Математические действия кроме деления и извлечения корня с обоими видами даёт целое.
- Самого большого числа для них нет — исчезает в бесконечности.

Отличия чисел
Наряду с общими признаками у этих понятий есть различия в написании, значениях и функциях.
Натуральные всегда больше ноля, целые — положительные, отрицательные и 0, поэтому не каждое целое будет натуральным.
У первых самое маленькое значение единица, у вторых его нет, оно бесконечно малое. Какую бы маленькую величину мы не придумали, от неё всегда можно отнять единицу и получить ещё меньшую и так бесконечно много раз.
Целыми легче описывать изменение количества, чем натуральными. При этом нет необходимости конкретно указывать увеличение или уменьшение численности. Само число характеризует эту перемену, а знак перед ним указывает направление. Вот примеры такого описания. Пусть в библиотеке есть некоторое количество книг. Если туда привезут еще восемьдесят, то их станет больше, а 80 выражает это изменение перечня в сторону повышения. Если же из библиотеки заберут тридцать книг, то их станет меньше, а 30 будет выражать перемену в сторону снижения. В библиотеку не будут привозить и увозить издания, то говорят о неизменности наличия литературы, то есть произошла нулевая перемена.
Этот пример показывает преобразование объёма книг с помощью целых чисел 80, −30 и 0 соответственно. Положительное 80 передаёт рост численности, отрицательное −30 выражает её понижение (отрицательная величина). Ноль показывает, что сумма предметов осталось без изменения.
Целыми хорошо описывается варьирование физических величин. При увеличении температуры на 3 градуса, это указывается значением 3. Уменьшение температуры на 10 градусов записывается как число с минусом: −10. А постоянство температуры определяется нолём.
Не каждый из нас математик, но понимание основ этой науки сыграет позитивную роль для каждого. Элементарные математические знания не раз выручат в трудной ситуации.
Натуральные и целые числа
Понятия натурального и целого числа. Арифметические операции над натуральными и целыми числами и их свойства. Делимость нацело. Основные законы арифметики
Понятие натурального числа возникло еще в древнем мире. В этом названии, происходящем от латинского слова natura — природа, отразилось представление, будто числа 1, 2, 3, 4, 5 и т.д. «созданы самой природой» — в отличие от дробей, отрицательных, иррациональных и тем более комплексных чисел, созданных человеком. На самом деле, конечно, натуральные числа — тоже творение человеческого ума. В современной математике натуральное число является понятием аксиоматическим, первичным. Существование натуральных чисел принимается без доказательства. В школьных учебниках обычно пишут, что натуральные числа — это числа, используемые в повседневной практике для счёта, т.е. 1, 2, 3, 4, 5,…,п,… Натуральные числа образуют множество, называемое множеством натуральных чисел и обозначаемое заглавной латинской буквой
(от французского слова «le nombre» — число). Запись означает, что число п принадлежит множеству натуральных чисел, т.е. является натуральным.
Более строгое описание понятия натуральных чисел, выходящее, впрочем, за пределы курса элементарной математики, опирается на аксиомы, сформулированные итальянским математиком Джузеппе Пеано (1858-1932). В них, в частности, используется понятие следования, принимаемое как первичное и не определяемое через другие понятия. Приведём указанные аксиомы Пеано для любознательного читателя:
- Единица есть натуральное число. Единица не следует ни за каким натуральным числом.
- Число, следующее за натуральным числом, есть натуральное число.
- Если натуральное число а следует за натуральным числом b и одновременно за натуральным числом С , то b и С тождественно равны.
- Если какое-либо предложение доказано для 1, и если из допущения, что оно верно для натурального числа а , вытекает, что оно верно для следующего за а натурального числа, то это предложение верно для всех натуральных чисел.
Последняя аксиома, называемая аксиомой полной индукции, лежит в основе известного метода доказательства — метода математической индукции.
Отметим некоторые из свойств натуральных чисел:
- Натуральных чисел бесконечно много.
- Множество натуральных чисел является упорядоченным, т.е. между любыми двумя натуральными числами а и b всегда можно поставить один и только один из трёх знаков сравнения: » = » (равно), « » (больше).
На множестве натуральных чисел вводятся четыре основные арифметические операции: сложения, вычитания, умножения, деления.
Опишем, как вводятся эти операции. Так, сложить два натуральных числа а и b значит найти в ряду натуральных чисел число С, находящееся на Ь -м месте от числа а :
Это число С называют суммой и обозначают а + b, а числа а , b при этом называют слагаемыми. Например, сложить числа 4 и 7 означает найти в натуральном ряду число, стоящее на седьмом месте по порядку, считая от числа 4, т.е. число 11. Таким образом, сумма состоит из стольких единиц, сколько их содержится в числах а и b . Заметим, что сумма двух (конечного числа) натуральных чисел существует всегда и сама является натуральным числом. В этом смысле принято считать, что множество N замкнуто относительно арифметической операции сложения.
Умножить натуральное число а на натуральное число b значит найти натуральное число С , равное сумме а чисел, каждое из которых есть b . Это число С называется произведением чисел а и b , и обозначается , а сами числа а , b при этом называются сомножителями. То есть произведение С состоит из стольких единиц, сколько их содержится в числе b , взятых столько раз, сколько единиц содержится в числе а . Произведение двух (конечного числа) натуральных чисел существует всегда и представляет собой также натуральное число, т.е. множество N замкнуто и относительно арифметической операции умножения.
На основании введённой на множестве натуральных чисел операции умножения можно определить понятие натуральной степени натурального числа. Так, если натуральное число а умножить само на себя п раз, где п — произвольное натуральное число, то такое произведение называют п -й степенью числа а и обозначают а» . Таким образом, по определению имеем
При этом число а называется основанием степени, а число п — показателем степени. При п = 1 полагают .
Определим теперь операции, обратные сложению и умножению натуральных чисел — действия вычитания и деления. Начнём с операции вычитания. Вычесть из натурального числа а натуральное число b значит найти число С такое, что сумма b + С равна а . Число С в этом случае называется разностью