Чем отличается определенный интеграл от неопределенного

Сегодня слово «Интеграл» можно услышать довольно часто, причем, зачастую, в самых неожиданных местах, например на биржевом канале по телевизору, или по новостям. Нередко мы слышим словосочетание «интегральные показатели» , слово «интегрированный», «интегративный» и тому подобное. Ну, по большому счету, чиновники и телеведущие, вообще, очень любят разные умные слова, правда вряд ли они понимают их истинное значение. А мы сегодня поговорим о том, что же такое интеграл, какие виды интеграла существуют и в чем их отличия.

Что такое интеграл

Интеграл- это латинское слово, которое пришло к нам из античности, и означает оно «Целый», или «Полный». То есть, ясно, что если про некий объект, например, сосуд молока говорили «интегер», это означало, что он полный, и молока в нем сколько было, столько и осталось.

Со временем это слово стали употреблять в совершенно разных дисциплинах- в философии, политике, экономике, в алгебре и геометрии. Но наиболее простую интерпретацию интегралу дает математика.

Итак, интеграл -это некая сумма отдельных частей. Вот наиболее простые примеры для, более четкого понимания сути этого термина:

Предмет — это интеграл(сумма) молекул.
Лист в клетку — это интеграл(сумма) клеток.
Солнечная система — это интеграл(сумма) солнца и планет.
Общество — это интеграл людей.
Отрезок- это интеграл (сумма) метров. Если маленький отрезок, то сантиметров, миллиметров или микроскопических отрезков.
Площадь какой-либо поверхности — это интеграл квадратных метров, квадратных сантиметров или миллиметров, а также микроскопических площадей.
Объем- это интеграл кубических метров или, как их еще называют — литров.

Что такое определенный и неопределенный интегралы?

Начнем с определенного, так как его смысл поддается пониманию легче.

Геометрия изучает площади. Например, если вы хотите поклеить дома обои, вам надо знать площадь стен, чтобы узнать, сколько обоев вы должны купить. Тогда вы просто умножаете длину стены на высоту и получаете ее площадь. В данном случае, эта площадь является интегралом квадратных метров или сантиметров, в зависимости от того, в каких единицах вы ее измеряли. Но поверхности, площадь которых нам требуется вычислить далеко не всегда имеют форму прямоугольника, квадрата, или даже круга. В большинстве случаев — это сложные фигуры с волнистыми сторонами. Наиболее распространенный пример — площадь фигуры под кривой, имеющей уравнение y=1/x . Дело в том, что найти ее площадь при помощи обычных формул, которыми мы находим площадь квадрата, круга или даже сферы — невозможно. Для этой цели был разработан определенный интеграл.

Суть метода в том, что нашу сложную фигуру нужно разбить на очень узкие прямоугольники, настолько узкие, что высота каждых двух соседних практически равна. Ясно, что по сути, можно уменьшать толщину этих прямоугольников бесконечно, поэтому для обозначения их толщины используется размер dx. X — это координата, а приставка d — это обозначение бесконечно уменьшаемой величины. Поэтому, когда мы пишем dx — это значит, что мы берем отрезок по оси x , длина которого очень мала, практически равна нулю.

Теперь поговорим о неопределенном интеграле. Только, для того, чтобы понять, что это такое, сначала нужно узнать о производной. Итак, начнем.

Производная — это угол наклона касательной к какому-либо графику в какой-нибудь ее точке. Иными словами — производная — это то, насколько график наклонен в данном его месте. К примеру, прямая линия в любой точке имеет один и тот же наклон, а кривая- разный, но он может повторяться. Для вычисления производной существуют специальные формулы, а процесс ее вычисления называют дифференцированием. Т.е. дифференцирование — это определение угла наклона графика в данной точке.

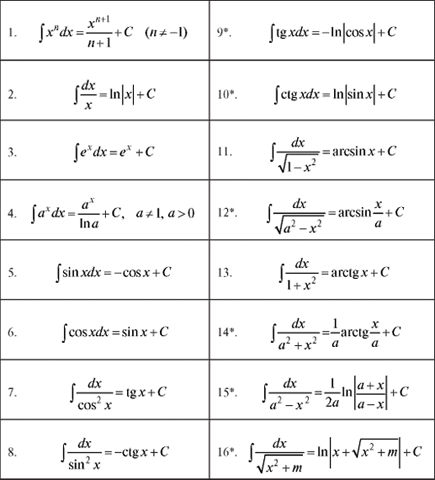
Таблица основных неопределенных интегралов

А для того, чтобы сделать наоборот — узнать формулу графика по углу ее наклона, прибегают к операции интегрирования, или суммирования данных обо всех точках. Интегрирование и дифференцирование- два взаимообратных процесса. Только здесь уже пользуются не тем интегралом, который был в первом пункте ( для определения площади ), а другим — неопределенным, то есть, не имеющим пределов.

Заключение

В заключение прорезюмируем, что основное отличие определенного интеграла от неопределенного — в их назначениях. Определенные интегралы используются для вычисления ограниченных параметров, таких как площадь, длина или объем, а неопределенный — при вычислении параметров, не имеющих границ, то есть функций.

Интересное видео на эту тему:

Интегралы – что это, как решать, примеры решений и объяснение для чайников

За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов

Почему вы не знаете, как решать интегралы

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

вычисление площади фигуры.
вычисление массы тела с неравномерной плотностью.
определение пройденного пути при движении с непостоянной скоростью.
и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Скидка 100 рублей на первый заказ!

Акция для новых клиентов! Разместите заказ или сделайте расчет стоимости и получите 100 рублей. Деньги будут зачислены на счет в личном кабинете.

Интеграл – что это?

Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

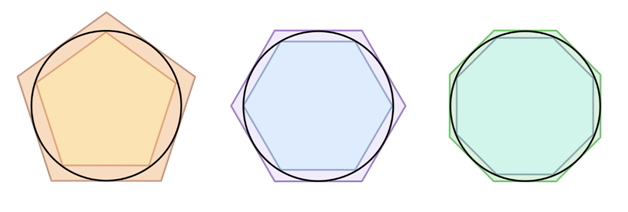
Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Объясняем понятие «Интеграл»

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».

Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.

Интеграл записывается так:

Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».

Определённый интеграл

В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.

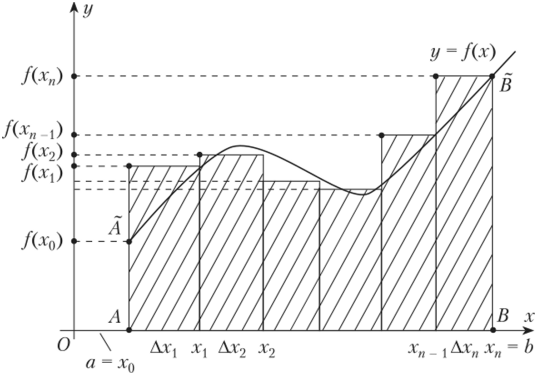
Точки A и B на оси X – есть ограничение зоны определения интеграла

Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:

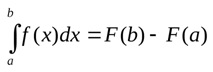
Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

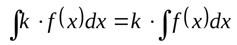
Разложение интеграла суммы на сумму интегралов

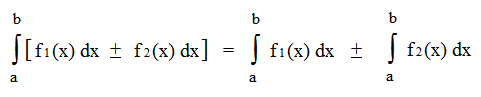
Если поменять местами a и b, знак изменится

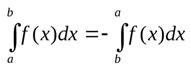
Можно разбить интеграл на промежутки следующим образом

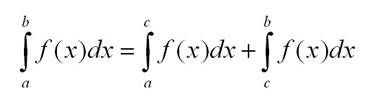
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

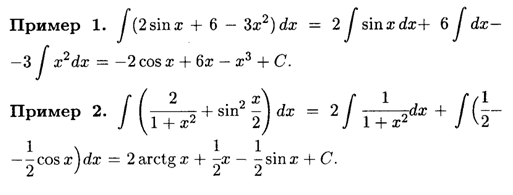
Решение определенного интеграла

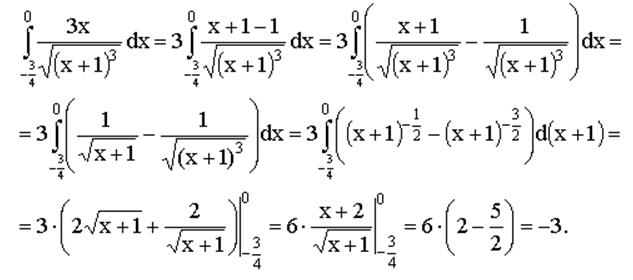
Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Первообразная. Неопределённый и определённый интегралы

Первообразная

Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого .

Операция нахождения первообразной функции f(x), называется интегрированием.

Неопределенный интеграл

Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.

Дифференциал-произвольное, бесконечно малое приращение переменной величины.

Свойства неопределённого интеграла

Таблица основных неопределённых интегралов

В виде

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.

Определённый интеграл

Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].

Общий вид определённого интеграла:

где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал

Свойства определённого интеграла: см. св-ва определённого интеграла.

Определённый интеграл вычисляется по формуле Ньютона –Лейбница:

Применение определённого интеграла:

1. Нахождение площади криволинейной трапеции

2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е

Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.

Решение:

3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.

Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.

Решение:

Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.

Что такое Интеграл

Интеграл — это математическая концепция, которая может быть двух типов:

неопределённый интеграл — это функция, которая получается интеграцией (это процесс, противоположный дифференцированию);
определённый интеграл выражает область, которая находится ниже кривой графика неотрицательной функции f и между любыми двумя значениями a и b.

Определённый интеграл выражает область под кривой графика неотрицательной функции f между любыми двумя значениями a и b, как показано на этом рисунке:

Интеграл, определённый между a и b, представлен как: f(x) dx

Неопределённый интеграл функции f — это другая функция F, полученная процессом, противоположным дифференцированию.

Дифференцирование в математике — это процесс, который превращает функцию f в другую функцию f’, называемую производной от f.

Например, нужно найти производную функции f(x) = cos x:

f’(x) = (cos x)’ = – sin x

Обозначение интеграла

Знак определённого интеграла:

Знак неопределённого интеграла: ∫

Основные свойства интегралов

Решение интегралов

Первообразная функция

Это функция, у которой производная функция равна исходной.

Функция F(x) является первообразной для производной функции f(x), если выполняется равенство F'(x) = f(x) (в диапазоне I).

F(x) = cos x — это первообразная функции f(x) = – sin x, т. к. (cos x)’ = – sin x;
F(x) = x³ — это первообразная функции f(x) = 3x², т. к. (x³)’ = 3x².

Важная деталь, о которой нужно помнить: первообразные функции не являются единственными! В предыдущем примере первообразная функции 3x² равна x³, но x³ + 1 также является первообразной той же функции (3x²), потому что (x³ + 1)’= 3x².

Это означает, что неопределённый интеграл функции f является множеством всех её первообразных функций и представлен так:

где С — произвольная постоянная.

Неопределённый интеграл

Неопределённый интеграл выглядит примерно так ∫ f(x) d(x) и обозначает множество всех первообразных некоторой функции f(x).

Если F — некоторая частная первообразная, то:

где С — произвольная постоянная.

Например, нужно вычислить неопределённый интеграл:

∫ (2x – 1) dx = ∫2x dx – ∫1dx = 2 (x²/2) – x + C = x² – x + C.

Определённый интеграл

Определённый интеграл выглядит примерно так: f(x) d(x).

С помощью определённого интеграла можно вычислить площадь геометрической фигуры, которая находится под кривой. Отрезок [a;b] называется отрезком интегрирования. Вместо a и b подставляются значения X (минимального и максимального). Например, как на этом рисунке:

Решение определённого интеграла (формула Ньютона-Лейбница):

f(x) dx = F(b) – F(a)

Например, нужно вычислить определённый интеграл:

(2 – x – x²) dx

1) Вычислить первообразную функцию

∫ (2 – x – x²) dx = 2x – x²/2 – x³/3 + C

2) Рассчитать верхний и нижний пределы (разницу между максимальным и минимальным значениями):

(2 – x – x²) dx = [2x – x²/2 – x³/3 + C] = [2(1) – 1²/2 – 1³/3 + C] – [2(-2) – (-2)²/2 – (-2)³/3 + C] = (2 – 1/2 – 1/3) – (-4 –2 + 8/3) = 2 – 1/2 – 1/3 + 4 + 2 – 8/3 = 9/2 = 4,5.

Относительно нашего примера график будет выглядеть таким образом (a = -2 и b = 1 (по оси x)):

Значит, площадь того, что закрашено на рисунке (под графиком), будет равна 4,5.

Неопределенный и определенный интеграл

Описание презентации по отдельным слайдам:

Описание слайда:

Неопределенный и определенный интеграл
Разработано преподавателем
математики Проскуряковой И.С.

Описание слайда:

Цели и задачи урока:
Дать понятие неопределенного интеграла
Изучить основные свойства неопределенного интеграла
Научить находить неопределенный интеграл
Дать понятие определенного интеграла
Формула Ньютона-Лейбница
Изучить основные свойства определенного интеграла
Геометрический смысл определённого интеграла

Описание слайда:

Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если для всех x из этого промежутка

Описание слайда:

Основное свойство первообразных
Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x).

Описание слайда:

Неопределенный интеграл
Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается

где C – произвольная постоянная
Символ  — знак неопределенного интеграла, означает операцию интегрирования заданной функции, которая называется подынтегральной функцией
— подынтегральное выражение
x — переменная интегрирования

Описание слайда:

Немного истории
«Интеграл» — латинское слово integro «восстанавливать» или integer – «целый».
Одно из основных понятий математического анализа,
возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным.
Впервые это слово употребил в печати шведский ученый Якоб Бернулли (1690 г.).

Описание слайда:

Символ был введен Лейбницем (1675г.).
Этот знак является изменением
латинской буквы S – первой буквы слова summa.

Описание слайда:

В развитии интегрального исчисления приняли участие русские математики:

В.Я. Буняковский
(1804 – 1889)
М.В. Остроградский
(1801 – 1862)
П.Л. Чебышев
(1821 – 1894)

Описание слайда:

Операции интегрирования и дифференцирования взаимно обратны и последовательное выполнение над некоторой функцией интегрирования и дифференцирования восстанавливает исходную функцию.

Описание слайда:

Свойства неопределенного интеграла

Описание слайда:

Таблица неопределенных интегралов

Описание слайда:

1. Давайте разобьем наш отрезок на n равных частей, отметим внутри отрезка [а;b] точки и через каждую точку проведем прямую параллельную оси ординат. Тогда наша фигура разобьется на n столбиков. Площадь трапеции будет равна сумме площадей столбиков.

Описание слайда:

a
b
x
y
0
В результате получим промежутки:
2. На каждом
выберем произвольную точку
3. Найдем
…
=
=
формула интегральной суммы

Описание слайда:

Опр: Если при любом разбиении отрезка
[a, b] на части и при любом выборе
точек на каждой части
интегральная сумма стремится к
одному и тому же пределу, то его
называют определенным интегралом
и обозначают:

Описание слайда:

Определенный интеграл.
Такой предел на самом деле существует, и для него было введено специальное обозначение и название – определенный интеграл. Важно! Определенный интеграл существует только в случае непрерывной или кусочно-непрерывной функции.
Определенный интеграл от непрерывной функции y=f(x) на отрезке [a;b] обозначается как

Читается как определенный интеграл от a до бэ эф от икс дэ икс.
Числа a и b – пределы интегрирования. (Нижний и верхний пределы).

Описание слайда:

Теорема: Если функция непрерывна на
отрезке [a, b], а функция
является первообразной для
на этом отрезке, то справедлива
формула:
формула Ньютона-Лейбница

Описание слайда:

Основные свойства определенного интеграла

Описание слайда:

Основные свойства определенного интеграла
а
b
с

Описание слайда:

Определенный интеграл.
Пример. Вычислить определенный интеграл

Решение. Первообразной для служит

Воспользуемся формулой Ньютона – Лейбница

Описание слайда:

Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:

Описание слайда:

Вычисление площадей
0
у
х
1
3
2
6
Пример. Вычислить площадь фигуры, ограниченной линиями
y=2x, x=1, x=3.
Решение.
Ответ: 8 кв.ед.

Описание слайда:

Пример. Вычислить площадь фигуры, ограниченной графиком функции y=cos(x) на отрезке [0;π/2].

Решение. Давайте построим график косинуса на нашем отрезке

Площадь полученной фигуры вычисляется с помощью определенного интеграла, гда a=0, b= π/2, f(x)=cos(x)

Описание слайда:

10.Вычислить определенный интеграл

11. Вычислить площадь фигуры, ограниченной функцией y=sin(x) на отрезке [2 π;3π].

12. Вычислить площадь фигуры, ограниченной линиями

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Математика
Презентации

Вам будут интересны эти курсы:

Курс повышения квалификации «Табличный процессор MS Excel в профессиональной деятельности учителя математики»
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс профессиональной переподготовки «Математика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Минпросвещения обсудит с экспертами развитие ученического самоуправления

Время чтения: 2 минуты

Учебный год начнется в традиционном формате

Время чтения: 1 минута

Робот-учитель от российских разработчиков будет обучать детей в индийской школе

Время чтения: 1 минута

Минпросвещения удвоило планы по числу школ, которые отремонтируют в 2022 году

Время чтения: 1 минута

В Петербурге создали программу для защиты детей в интернете

Время чтения: 3 минуты

Вырос средний балл поступающих в педагогические вузы России

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.