Чем отличается темп роста от темпа прироста?

Показатели динамики: темп роста и темп прироста

Темп роста

Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр). Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения. Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.

Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста

Коэффициент роста может быть рассчитан по формулам:

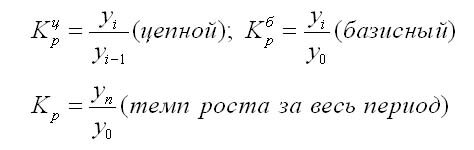
Также темп роста может определяться так:

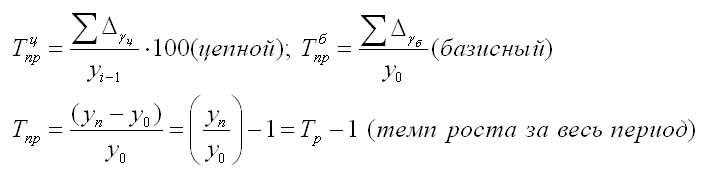
Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.

Абсолютный прирост

Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:

1. Абсолютный прирост (цепной):

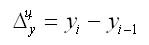
2. Абсолютный прирост (базисный):

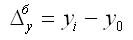
где уi — уровень сравниваемого периода;

Уi-1 — Уровень предшествующего периода;

У0 — уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:

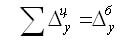
Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.

Темп прироста

Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:

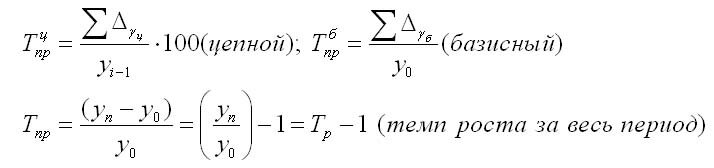
Темп прироста можно получить из темпа роста:

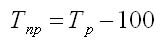
Коэффициент прироста может быть получен таким образом:

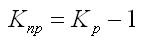
Абсолютное значение 1%-го прироста

Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:

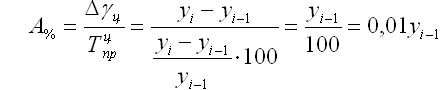
Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

Примеры расчетов показателей динамики

Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики

О показателях динамики

При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.

Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста. Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения. Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.

Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем. В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными. Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.

СПИСОК ЛИТЕРАТУРЫ ОНЛАЙН

Как рассчитать темп роста и прироста?

Темп роста — это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).

Темп прироста — это прирост какой либо изучаемой величины за один временной период за вычетом 100%.

Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста — всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.

Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.

Расчет темпа роста и прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

На рисунке представлен пример расчета темпа роста и прироста:

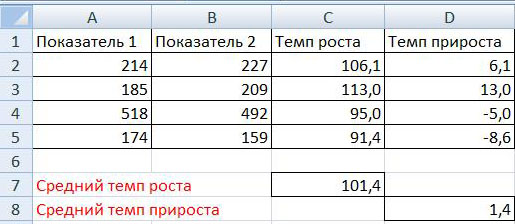
Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:

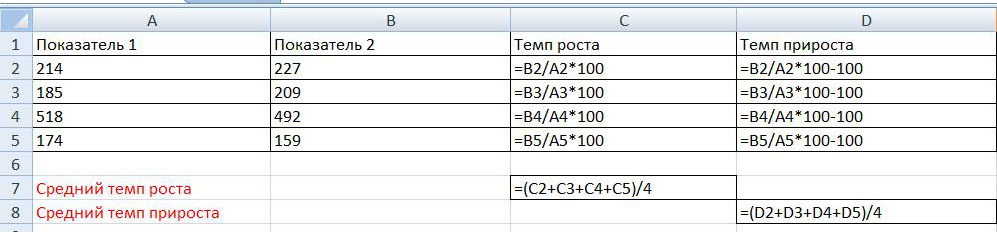
На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.

Расчет средних темпов роста и прироста

Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста — сумма темпов прироста за все периоды делится на количество периодов.

Расчет базисного темпа роста и базисного темпа прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста. Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов — формулы расчета темпа роста и прироста.

На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):

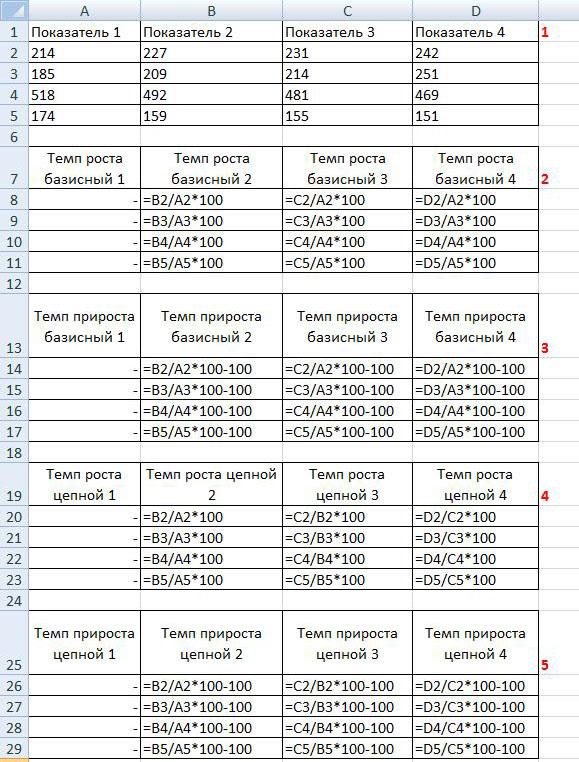
Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя.

В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.

Расчет цепного темпа роста и цепного темпа прироста

На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).

Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей. Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя.

То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.

Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:

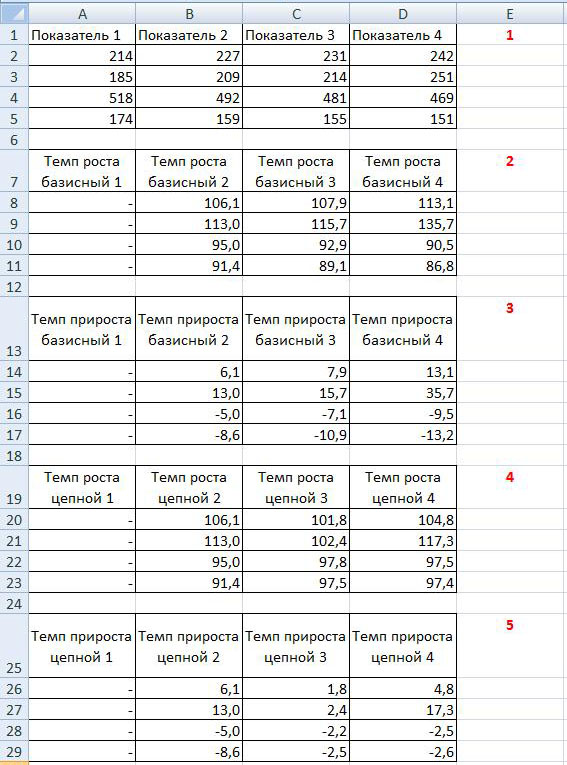
Обратите внимание, что при расчете базисного и цепного показателей, значения базисного и цепного темпов роста и прироста равны, так как при избрании в качестве базисного показателя первого из ряда, они рассчитываются одинаково.

Темпы роста и прироста.

Поможем написать любую работу на аналогичную тему

Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени.

С этой целью для динамических рядов рассчитывают ряд показателей:

— абсолютные приросты;

— темпы прироста.

Темп роста — относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: , либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем , выбранным за базу сравнения: . Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.

Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.

Темп прироста — относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.

Базисные темпы прироста: .

Цепные темпы прироста: .

и — абсолютный базисный или цепной прирост;

— уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;

— уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.

Существует связь между темпами роста и прироста:

К = К — 1 или К = К — 100 % (если темпы роста определены в процентах).

Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый — абсолютное значение одного процента прироста: .

Чем отличается темп роста от темпа прироста?

Анализ социально-экономических явлений, так или иначе, сводится к изучению динамики. Для этого используют аналитические показатели, с помощью которых оценивают текущие отклонения, а также прогнозируют состояние исследуемых явлений в будущем. К таким характеристикам относятся темпы роста и прироста. Они помогают наглядно продемонстрировать развитие рассматриваемого процесса во времени.

Темп роста

Когда говорят: «Объем продаж вырос на 25 %», то подразумевают как раз темп роста. Любой учебник статистики определяет его как интенсивность изменения уровней динамического ряда, которое выражается через отношение количественных значений, принадлежащих разным временным интервалам.

В математике отношение представляет собой деление одного числа на другое. Например, в прошлом году объем продаж составлял 2 млн. рублей, в текущем году 2,5 млн. Если разделить значение текущего года на значение предыдущего, то образуется некоторый коэффициент: 2,5 / 2 = 1,25. Это и есть темп роста. Коэффициенты можно выражать в процентах. Умножим 1,25 на 100%, получим 125%.

На основе процентного соотношения судят о характере отклонений. Если процент превышает 100, то говорят об увеличении исследуемого параметра. Если при расчете результат будет меньше 100, то говорят о снижении уровня. В примере выше объем продаж вырос на 25 %. А что, если наоборот? Пусть в прошлом году объем реализации составлял 2,5 млн. рублей, а в текущем 2 млн. Тогда, разделив 2 на 2,5, получим 0,8 или 80%. Что меньше 100% на 20%. Таким образом, спад объема реализации продукции составит 20%.

Бросается в глаза несоответствие: произведены математические манипуляции с одними и теми же числами 2 и 2.5, а получены разные отклонения — повышение на 25%, а снижение на 20%. Это объясняется тем, что одно и то же числовое значение составляет разную величину доли для каждого случая. И действительно, если рассудить, то сэкономленный рубль дороже заработанного.

Аналитические показатели динамики вычисляют для целого ряда данных, характеризующих социально-экономическое явление или процесс в течение длительного периода времени. Интересно увидеть изменение размера продаж не за один год, а скажем, лет за десять. Годовые темпы роста, рассчитанные на протяжении долгого периода, дают общее представление о характере варьирования исследуемой величины. Полученная тенденция (тренд), берется за основу для прогнозирования явления в будущем.

При сравнении двух соседних количественных значений в динамическом ряду, то есть текущего и прошлого, прошлого и позапрошлого годов, получают цепные темпы роста, то есть, рассчитанные «по цепочке». Если производится сравнение одного и того же уровня, выбранного в качестве базы сравнения, с другими – текущим, предыдущим, то такие темпы роста называют базисными.

1. Более поздний по времени показатель делят на более ранний.
2. Бывает, что темп роста равен 100 %. Это означает, что величина с течением времени не изменилась, при делении одинаковых чисел получается единица.
3. Этот параметр всегда больше нуля.
4. Повышение и снижение определяются исходя из сравнения с уровнем единицы (100%).

Темп прироста

Расчет темпа прироста проходит в два этапа. Сначала вычисляют разность двух соседних уровней в динамическом ряду: текущего и предыдущего года. А затем, полученное значение абсолютного отклонения делят на уровень предшествующего периода. На примере это выглядит так. Объем продаж в текущем году 2,5 млн., прошлогодний объем ─ 2 млн. Прирост будет равен: (2,5 — 2) : 2 = 0,25. Можно умножить на сто, тогда получится 25%. Это означает, что продажи выросли на 25 % по сравнению с предыдущим годом.

Из примера видно, что темп прироста соответствует процентному изменению количественной характеристики текущего периода по отношению к предыдущему. В учебной литературе так и сказано: «характеризует абсолютный прирост в относительных величинах». Этот коэффициент также может быть цепным и базисным.

Очевидна связь между аналитическими показателями динамики. В примере темпы роста и прироста составляют 125% и 25% соответственно. Можно с уверенностью утверждать, что эти относительные характеристики отличаются друг от друга на 100%.

В принципе, и тот и другой параметр дают представление об изменении изучаемой величины во времени.

Отличие темпов роста и прироста

Справедливо возникает вопрос. Если темпы роста и прироста отражают одинаковое отклонение изучаемой величины, то почему существует два параметра? И есть ли различие между ними?

Безусловно, есть. С точки зрения математики, темп роста получают путем деления двух положительных чисел, и результат будет всегда больше нуля. При вычислении темпа прироста в числителе берут абсолютное отклонение величин. И если наблюдалось увеличение уровня, то в числителе абсолютный прирост будет со знаком плюс. А при снижении, абсолютное изменение будет с минусом, тогда и сам прирост будет минусовым. Этим и отличаются данные показатели.

Таким образом, темп роста всегда положителен, и подъем или снижение уровня определяется относительно 100%. Темп прироста может быть как положительным, так и отрицательным. А увеличение или уменьшение определяется по знаку полученного коэффициента.

Все хорошо в теории, но на практике бывают моменты, когда расчет показателей динамики вызывает трудности. Например, в настоящее время прибыль составила 2,5 млн. денежных единиц, а в прошлом году прибыли не было совсем, предприятие потеряло 2 миллиона. Фактически прибыль составила -2 млн. денежных единиц. Получается, что приходится делить положительное число на отрицательное. И тогда темп роста тоже будет с минусом. А этого не может быть. Как здесь поступить, куда девать минус? Получается, что относительные показатели динамики теряют смысл и не могут иметь экономической интерпретации. В таком случае вычисляют только абсолютное отклонение уровня: 2,5 — (-2) = 4.

В принципе, можно пойти обходным путем, и привести уровни к некоторой базе, которая принимается равной наименьшему значению. Остальные количественные характеристики следует пересчитать относительно этой базы сравнения. В примере уровень с отрицательным значением (число -2) примем за 1. Тогда величина периода с положительной прибылью (число 2,5) после приведения к базе сравнения будет равна: (2,5 — (-2)) + 1 = 5,5.

Теперь можно переходить к исчислению роста: (5,5 / 1) * 100 = 550% и прироста: ((5,5 — 1) / 1) * 100 = 450%. Итак, прибыль выросла на 450% или в 4,5 раза. Такой подход в расчете еще раз подтверждает важность выравнивания уровней динамического ряда перед проведением статистического анализа.

Вычисление параметров роста и прироста необходимо для составления полного представления о развитии исследуемого явления во времени. Понимание принципов расчета аналитических показателей динамики упростит восприятие экономических и статистических данных, транслируемых СМИ.

Формула темпа роста

Чтобы проанализировать деятельность компании за несколько периодов, аналитики используют такие показатели, как темпы роста и темпа прироста. С их помощью изучают прибыль, продажи всей компании и отдельных сотрудников. Оба показателя демонстрируют динамические изменения текущего периода по сравнению с прошлым.

Главная причина, почему нужно считать темп роста – это желание укрепить свои позиции на рынке. Уже доказано, что если компания рационально распределяет свои ресурсы и денежные средства, то ей проще добиться идеальной экономической модели. То есть эффективно управлять финансами, сохранять оптимальное соотношение между задолженностями. Для этого необходимо постоянно контролировать коэффициент стабильности развития. Он зависит от регулярного и прогнозируемого экономического роста.

Темпы роста доходов и прибыли особенно интересны инвесторам. Так что, если в обозримом будущем фирме могут понадобиться дополнительные средства, уже сейчас следует оценить организацию с точки зрения привлекательности для инвестиций.

Вторая причина уже сейчас начать вычисления – необходимость увеличить прибыль. Если компания ставит перед собой такую цель по технике SMART, она обязана регулярно проверять достижение цели. Для этого она регулярно рассчитывает, насколько увеличилась ее прибыль.

На основе этого показателя в том числе судят об успешности всего бизнеса. Бывает так, что продажи растут количественно, то есть с каждым месяцем компания реализует больше товаров. Но прибыль может сокращаться.

Что такое темп роста и прироста

По сути, вычисление темпа роста – это поиск процентного соотношения между двумя показателями: текущим и прошлым, взятым за основу. Таким образом, для расчета можно использовать базовую формулу:

Значение выбранного показателя за текущий период / Значение выбранного показателя за прошлый период

Чтобы получить результат, можно провести только деление двух показателей. Тогда итог будет выражен в относительной величине. Также результат деления можно умножить на 100 % и получить темп роста в процентах. Тогда значение оценивается так:

• если оно превышает 100 %, то в компании наблюдается рост;
• если оно равно 100 %, то никаких изменений не произошло;
• если оно меньше 100 %, то наблюдается спад.

Темп роста зависит от типа роста. Их существует два: экстенсивный и интенсивный. В первом случае увеличение объемов зависит от увеличения использования сырья, привлечения большего количества работников или установки большего количества оборудования. За счет этого у компании получается производить больше товаров, чем раньше. Чем больше товаров создано, тем больше реализовано. Следовательно, растет прибыль и продажи. Однако со временем возникает технический застой, производство снижается и темп роста стремится к нулю.

Во время интенсивного роста все показатели – сырье, оборудование, рабочая сила – остаются прежними. Однако увеличивается качество. Например, оборудование начинает работать по новой программе, меняется поставщик сырья. В результате компания производит то же количество товаров, что и раньше, но продукты становятся более качественными, надежными. Благодаря этому клиенты покупают больше и компания получает прибыль.

Особенность интенсивного роста заключается в том, что первое время показатель темпа роста может даже снизиться. Однако это лишь временная перестройка: это не значит, что развитие фирмы замедлилось.

Три вида темпа роста

Оба показателя (и Тр, и Тпр) могут быть получены разными способами. Это зависит от целей анализа. Например, базисный способ основан на выборе основы или базы. После определения базы выбирается текущий показатель и вычисляется соотношение между ними. По сути, вычисление дублирует основную формулу:

Выбранный показатель / Базовый показатель * 100 %

Второй вид – цепной Тр. Использовать такое вычисление необходимо, чтобы увидеть изменения показателя в динамике. Иначе говоря, формула ЦТр позволяет увидеть, как отличается каждое последующее значение от предыдущего, а предыдущее – от того, которое было перед ним.

Тогда темп роста вычисляется так:

Выбранный показатель / Предыдущий показатель * 100 %

Каждое следующее соотношение вычисляется отдельно, по цепочке, пока не будет достигнуто базовое, начальное значение.

Существует средний темп роста. Он необходим, когда уже вычислены значения за разные периоды (например, за три и более месяцев) и требуется найти среднее значение роста. Для этого нужно найти среднее геометрическое от всех показателей. Также есть более простая формула, которая основана на среднем арифметическом значении:

(Тр1 + Тр2 + … + ТрN) / N

В этой формуле Тр1 обозначает темп роста за первый период (например, за январь), Тр2 и Тр3 – показатель за второй и третий периоды (например, за февраль и март соответственно). ТрN – темп роста за последний период, участвующий в вычислении. Естественно, в формулу можно подставить неограниченное количество показателей, тогда изменится и число, на которое делится сумма.

Значение можно получить по второй, усложненной формуле. Она называется GAGR и выглядит так:

((Текущий показатель / Прошлый показатель) * (1 / N)) — 1

В этой формуле N – это количество лет, которое взято для изучения.

У усложненной формулы есть преимущество. Она позволяет четче увидеть среднегодовой рост прибыли нежели при вычислении обычного среднего арифметического.

Темп прироста

Часто вместе с темпом роста рассчитывают темп прироста. Если Тр показывает сам факт изменений, то Тпр демонстрирует, насколько выросло или уменьшилось за заданный период. Дополнительный показатель необходим, чтобы лучше судить о работе компании и реализации ее стратегии. Вот такая формула используется:

(Текущее значение — Базовое значение) / Базовое значение * 100 % — 100 %

Если получился отрицательный результат, значит, показатель уменьшился.

Темп прироста тоже может быть цепным или базисным. Чтобы вычислить базисный, потребуется использовать такой метод:

Показатель за данный период / Базовый показатель * 100 % — 100

Цепной ТПр рассчитывает по формуле, аналогичной цепному ТР:

Текущий показатель / Показатель за прошлый период * 100 % — 100

Чтобы вычислить средний ТПр, потребуется просто вычесть 100 из среднего ТР.

Нюансы вычислений

Все формулы на первых взгляд очень похожи. Из-за этого неопытные сотрудники часто путаются между разными видами темпа роста, а также между ростом и приростом. Вот нюансы, которые нужно учитывать – они помогут правильно провести расчет:

• темп роста показывает долю, которую составляет одно число внутри другого;
• прирост показывает разницу между двумя числами;
• зная Тр, можно вычислить прирост. Однако в обратном порядке это правило не работает.

Самым спорным нюансом остается возможность получить в результате расчетов отрицательное значение. Считается, что Тр не может получится отрицательным. Но в экономике такое иногда происходит. Например, в продажах это сигнализирует, что наступил спад и снижение прибыли. При анализе изменения ВВП или доходов на человека отрицательный результат говорит о начале кризиса.

Связь Тр и других финансовых показателей

Если необходимо рассчитать темп роста прибыли, то для анализа придется обращаться к другим показателям. Прежде всего это выручка, то есть весь объем продаж компании. Показатель считается наиболее объективным, так как всегда одинаков, вне зависимости от того, какая учетная система используется для подсчета данных. Выручка – доступна для анализа, для ее вычисления не требуются сложные формулы и учет косвенных затрат, в отличие от другого важного – чистой прибыли.

Однако на основе только выручки не получится составить объективную картину о росте и развитии компании. Ее стоит анализировать в совокупности с другими финансовыми показателями. Например, с EBITDA – прибылью, которая получается до того, как будут вычтены затраты на налоги, амортизацию и проценты. EBITDA – это не только наиболее близкий показатель к сумме финансового потока, но и простой способ вычислить стоимость всего предприятия.

Пример расчета

Использовать указанную формулу можно для анализа продаж, объемов производства и даже зарплаты сотрудников. Например, работник получает гонорар и он зависит от производительности. За январь работник получил 30 тысяч рублей, а за февраль 35 тысяч рублей. Используя формулу темпа роста, можно вычислить показатель: 35000 / 30000 * 100 % = 116 %. Февральский гонорар относительно предыдущего месяца составляет 116 %.

Также можно рассчитать темп прироста. Тогда в соответствии с формулой получаются такие расчеты: (35000 — 30000) / 30000 * 100 % — 100 % = 16 %.

Таким же образом можно просчитать прибыль и темпы ее изменения. Например, в компании такой объем продаж наблюдается в разных периодах:

• первый квартал – 300 тысяч рублей;
• второй квартал – 320 тысяч рублей;
• третий квартал – 260 тысяч рублей;
• четвертый квартал – 310 тысяч рублей.

Вот как будут выглядеть расчеты базисного темпа:

• первый квартал принимается за 100 % или за базу. На основании этих данных будут вестись дальнейшие расчеты;
• БТр во втором квартале равен 320 тысяч / 300 тысяч * 100 %, то есть 106 %;
• БТр в третьем квартале снова рассчитывается, исходя из данных за первый квартал. То есть – 260 тысяч / 300 тысяч * 100 % = 86 %;
• аналогично считается базисный Тр по четвертому кварталу – 310 тысяч / 300 тысяч * 100 % = 103 %.

Затем можно вычислить цепной темп роста:

• так как первый квартал года – это начало отсчета, то вычислить цепной Тр не получится;
• во втором квартале он равен – 320 тысяч / 300 тысяч * 100 % = 106 %. То есть фактически это значение дублирует базисный Тр;
• в третьем периоде значение составляет 260 тысяч / 320 тысяч * 100 % = 81 %;
• в четвертом квартале цепной темп роста считается так – 310 тысяч / 260 тысяч * 100 % = 119 %.

На основании полученных значений можно делать выводы и искать причины колебаний. Например, базисные темпы колебались в третьем периоде – там наблюдался самый низкий прирост. Возможно, это было связано с сезонностью продаж или окончанием временной акции.