В чем разница между центробежной и центростремительной силой
Центростремительная и центробежная силы
Центростремительная и центробежная силы
Центростремительная и центробежная силы
В буквальном смысле эти силы выглядят как определённым способом ориентированные по отношению к центру — некой точке, равноудалённой от всех точек траектории движущегося тела. В двумерном пространстве (на плоскости) такой траекторией является окружность, а в трехмерном — тоже окружность, образованная пересечением сферической поверхности плоскостью, в общем случае не проходящей через её центр.
Все остальные траектории любого вида центром в этом смысле не обладают, и потому применительно к движущемуся по не круговым траекториям телу использование представления о центростремительной и центробежной силах не оправдано и ведёт к многочисленным недомолвкам и недоразумениям.

Центростремительная сила — сила, действующая со стороны неких связей, ограничивающих свободу движения тела, и вызывающая его поворот вокруг центра поворота. Природа связей может быть любой, если они обладают свойством увеличивать потенциальную энергию системы тело-связь при удлинении последней.
Реально существующей является лишь сила реакции связи. Центростремительная, равно как и центробежная сила, как самостоятельная сила, не существует и представляет собой лишь результат формального разложения реальной силы на две составляющие.
В случае установившегося движения тела (вращения) центростремительная сила совпадает с силой, представляющей собой реакцию связи , она направлена перпендикулярно к вектору его скорости, работы не совершает, кинетическая энергия движения тела не изменяется и такое движение может продолжаться неограниченно долго.
В случае неустановившегося движения по кривой (например при раскрутке пращи), траектория движения тела представляет собой спираль и центростремительная сила, по определению нормальная по касательной к траектории, направлена в сторону мгновенного центра вращения и представляет собой результат формального разложения реальной силы реакции связи на две. При этом работу совершает тангенциальная составляющая силы реакции связи, ведущая к изменению кинетической энергии тела (при разгоне) или уменьшению её (при торможении). Это периодически имеет место в Мировом пространстве при движении небесных дел по кеплеровским эллиптическим орбитам вокруг общего центра тяготения
Центробе́жная си́ла — сила, действующая со стороны испытывающего поворот тела на вызывающие этот поворот связи, равная по модулю центростремительной силе и всегда направленная в противоположную ей сторону (Третий закон Ньютона). Применяемый не к связям, а, наоборот, к поворачиваемому телу, как объекту своего воздействия, термин Центробежная сила (букв. Сила, приложенная к поворачивающемуся или вращающемуся материальному телу, заставляющего его бежать от мгновенного центра поворота), есть эвфемизм, основанный на ложном толковании первого закона (принципа Ньютона) [1] в форме :
Всякое тело сопротивляется изменению своего состояния покоя или равномерного прямолинейного движения под действием внешней силы
Всякое тело стремится сохранять состояние покоя или равномерного прямолинейного движения до тех пор, пока не подействует внешняя сила.
Отголоском этой традиции и является представление о некоей силе, как о материальном факторе, реализующем это сопротивление или стремление. О существовании такой силы уместно было бы говорить, если бы, например, вопреки действующим силам, движущееся тело сохраняло бы свою скорость, но это не так. [3]
Первый закон Ньютона, нередко называемый принципом и потому допускающим различия в словесной формы его выражения, сводится к утверждению, что природа вещей такова, что скорость движения материальной точки, как по величине, так и по направлению в некоторой системе отсчёта (сам Нютон связывал её с эфиром, заполняющим всё пространство) [4] , остаётся постоянной, но начинает изменяться тотчас, как возникает на то причина, называемая силой.
Рассматриваемое тело с массой (точнее — инертной массой) m приобретает отличающееся от нуля ускорение a в тот же момент t = 0 , когда начинает действовать на него сила F . (Второй закон Ньютона :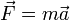 ) Однако для достижения отличающейся от нуля скорости v требуется некоторое время t в соответствие с определением импульса силы : t = mv / F .Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила. [5]
) Однако для достижения отличающейся от нуля скорости v требуется некоторое время t в соответствие с определением импульса силы : t = mv / F .Или, иначе, скорость тела не изменяется сама по себе, без причины, но она начинает изменяться тотчас, как на него начинает действовать сила. [5]
Использование термина Центробежная сила правомочно тогда, когда точкой её приложения является не испытывающее поворот тело, а ограничивающее его движение связи. В этом смысле Центробежная сила представляет собой один из членов в формулировке Третьего закона Ньютона, антагониста Центростремительной силе, вызывающей поворот рассматриваемого тела и к нему приложенной. Обе эти силы равны по величине и противоположны по направлению, но приложены к разным телам и потому не компенсируют друг друга, а вызывают реально ощутимый эффект — изменение направление движения тела (материальной точки).
Оставаясь в инерциальной системе отсчёта, рассмотрим два небесных тела, например, компонента двойной звезды с массами одного порядка величины M1 и M2 , находящихся на расстоянии R друг от друга. В принятой модели эти звёзды рассматриваются как материальные точки и R есть расстояние между их центрами масс. В роли связи между этими телами выступает сила Всемирного тяготения FG:GM1M2 / R 2 , где G — гравитационная постоянная. Это — единственная здесь действующая сила, она вызывает ускоренное движение тел навстречу друг другу.
Однако, в том случае, если каждое из этих тел совершает вращение вокруг общего центра масс с линейными скоростями v1 = ω1 R1 и v2 = ω2 R2 , то подобная динамическая система будет неограниченное время сохранять свою конфигурацию, если угловые скорости вращения этих тел будут равны: ω1 = ω2 = ω , а расстояния от центра вращения (центра масс) будут соотноситься, как: M1 / M2 = R2 / R1 , причём R2 + R1 = R , что непоcредственно следует из равенства действующих сил: F1 = M1a1 и F2 = M2a2 , где ускорения равняются соответственно: a1 = ω 2 R1 и a2 = ω 2 R2 [6]
Центростремительные силы, вызывающие движение тел по круговым траекториям равны (по модулю): F1 = F2 = FG . При этом первая из них является центростремительной, а вторая — центробежной и наоборот: каждая из сил в соответствие с Третьим законом является и той, и другой.
Поэтому, строго говоря, использование каждого из обсуждаемых терминов излишне, поскольку они не обозначают никаких новых сил, являясь синонимами единственной силы — силы Всемирного тяготения. То же самое справедливо и отношении действия любой из упомянутых выше связей.
Однако, по мере изменения соотношения между рассматриваемыми массами, то есть всё более значительного расхождения в движении обладающих этими массами тел, разница в результатах действия каждой из рассматриваемых тел для наблюдателя становится всё более значительной.
В ряде случаев наблюдатель отождествляет себя с одним из принимающих участие тел и потому оно становится для него неподвижным. В этом случае при столь большом нарушении симметрии в отношении к наблюдаемой картине, одна из этих сил оказывается неинтересной, поскольку практически не вызывает движения.
Переписывая Второй закон в виде F − ma = 0 и заменяя второй член слева на некую силу Fi = − ma , получаем новую запись Второго закона: F + Fi = 0 .Здесь обе силы действуют на одно и то же тело, причём их сумма равна нулю, из чего следует, что данное тело в системе отсчёта, связанной с этим телом, покоится, хотя сама система вместе с ним движется ускоренно. Эта сила Fi , ничем не отличается по своему происхождению от силы F (о чём говорит знак равенства в канонической записи закона). Существует предложение называть её Ньютоновской силой инерции. Никакого отношения к центробежной силе эта сила не имеет. [5]
В чем разница между центробежной и центростремительной силой


Рис. 4.8
В каждый момент времени камень должен был бы двигаться прямолинейно по касательной к окружности. Однако он связан с осью вращения веревкой. Веревка растягивается, появляется упругая сила, действующая на камень, направленная вдоль веревки к центру вращения. Это и есть центростремительная сила (при вращении Земли вокруг оси в качестве центростремительной силы выступает сила гравитации).
 но так как
но так как  то
то
 |
(4.5.2) |
 |
(4.5.3) |
Сила же, приложенная к связи и направленная по радиусу от центра, называется центробежной.
Помните, что центростремительная сила приложена к вращающемуся телу, а центробежная сила – к связи.

Сила гравитационного притяжения направлена к центру Земли.
Сила реакции опоры (нормального давления) направлена перпендикулярно к поверхности движения.
Центробежная сила – сила инерции первого рода. Центробежной силы, приложенной к вращающемуся телу, не существует.
С точки зрения наблюдателя, связанного с неинерциальной системой отсчета, он не приближается к центру, хотя видит, что Fцс действует (об этом можно судить по показанию пружинного динамометра). Следовательно, с точки зрения наблюдателя в неинерциальной системе есть сила, уравновешивающая Fцс, равная ей по величине и противоположная по направлению:


| Fцб = m ω 2 R. | (4.5.4) |

Рис. 4.9
R = RЗ cosφ φ – широта местности);  ω – угловая скорость вращения Земли.
ω – угловая скорость вращения Земли.
Сила тяжести есть результат сложения двух сил:  и
и  , таким образом g (а значит и mg ) зависит от широты местности:
, таким образом g (а значит и mg ) зависит от широты местности:
 ,
,
где g = 9,80665 м/с2 – ускорение свободного падения тела. Направлено g точно к центру только на полюсе и на экваторе.
Центростремительная и центробежная сила
Центростремительная и центробежная сила. Тело может описывать окружность около некоторого центра только в том случае, если на это тело действует сила, направленная к центру и равная mv 2 /r где m — масса тела, v — его скорость, r — радиус окружности. Эта сила называется центростремительной. Если, например, спутник описывает окружность около планеты, то ньютоновское притяжение спутника к планете играет роль центростремительная и центробежная сила; оно может быть выражено вышеуказанной формулой. В других случаях источником центростремительной и центробежной силы может являться какое-нибудь тело, которое своим давлением или натяжением постоянно отклоняет тело, описывающее окружность, от того прямолинейного пути, по которому тело двигалось бы вследствие инерции. Например, если вагон движется по закруглению, он стремится по инерции слететь с рельсов и продолжать движение по касательной; рельсы давлением, которое они производят на колеса вагона, сворачивают его с прямого пути и заставляют описывать дугу: давление рельсов на колеса есть центростремительная и центробежная сила. Точно так же, когда математический маятник (см. XXVIII, 358) описывает дугу в вертикальной плоскости, то на его шарик действует центростремительная и центробежная сила, которая берется из натяжения нити. Применяя 3-ий закон движения (см. XVIII, 42), приходим к выводу, что с какой силой рельсы давят на колеса вагона, с такой же силой и колеса давят на рельсы в противоположную сторону (т. е. от центра к окружности); далее, с какой силой натяжение нити маятника действует (по направлению к центру окружности) на шарик, с такой же силой и шарик тянет нить от центра. Вообще, если круговое движение тела осуществляется благодаря наличию некоторого препятствия, ограничивающего свободу движения тела, то наряду с «действием» препятствия на тело — центростремительная и центробежная сила — существует «противодействие» тела на препятствие. Это противодействие называется центробежной силой. Центростремительная и центробежная сила, по 3-му закону движения, всегда равна центробежной силе (следовательно, выражается формулой mv 2 /r), но направлена от центра.
Кроме такого понимания центростремительной и центробежной силы, существует еще другое, которое можно разъяснить на следующем примере. Пусть чертеж изображает сечение земного шара по одному из меридианов. N и S —полюсы, EQ —экватор, KL — параллель на широте φ. Пусть на этой параллели в точке К находится некоторое тело, подвешенное на нити (например, грузик отвеса). Если бы земля не вращалась, то это тело под действием силы КР ньютоновского тяготения (см. XLII, 1) стремилось бы к центру земли; нить своим натяжением уравновешивала бы эту силу и, значит, приняла бы направление радиуса КО. На самом же деле земля вращается около оси NS, вследствие чего тело К описывает окружность радиуса КС. Необходимая для такого движения центростремительная и центробежная сила KS, величину которой нетрудно вычислить по формуле mv 2 /KC, берется, как составляющая, из приложенной к телу силы КР; другая же составляющая KR уравновесится натяжением КТ нити, которая поэтому и расположится по продолжению KR 1) . Сила KR есть «сила тяжести», или «вес» тела; нахождение ее величины есть главная цель, которой служит предшествующее рассуждение. Но этой цели можно достигнуть несколько иначе, рассматривая вес тела KR не как разность (геометрическую, см. VIII, 154) сил КР и KS, но как равнодействующую силы КР и фиктивной силы КМ, равной и противоположной центростремительной и центробежной силе KS. Эта фиктивная сила опять-таки называется центростремительной и центробежной силой (во втором понимании). Существенное различие обоих пониманий заключается в том, что в первом случае центростремительная и центробежная силы приложены к разным телам, тогда как во втором случае они приложены к одному и тому же телу. Поэтому оба понимания центростремительной и центробежной силы несовместимы.
1) Мы имеем здесь пример часто встречающегося в физике разложения силы, приложенной к телу, по правилу параллелограмма на две составляющих силы, из которых одна двигает тело, а другая уничтожается его связями. Другой подобный пример дается наклонной плоскостью (см. XXIX, 552).
Центробежную силу во втором понимании мы назвали фиктивной. Но при известных условиях ее возможно было бы рассматривать как реальную. Так, если бы земные физики были чужды представления о вращении земли около оси, то, наблюдая изменение силы тяжести с широтой (см. ХLII, 3), они могли бы придти к выводу, что сила тяжести есть равнодействующая силы, соответствующей тяготению, и силы КМ; с их точки зрения эта сила КМ была бы реальной.
Второе понимание центробежной силы само по себе имело бы малую ценность, если бы оно не представляло собой частного применения весьма общего механического принципа — т. н. принципа Даламбера (см. XVII, 523). Этот принцип позволяет динамические задачи о движении заменять (более простыми) задачами о равновесии, при чем нужно только к каждой движущейся материальной точке приложить фиктивную «силу инерции», равную произведению массы точки на имеющееся у ней ускорение и направленную в сторону, противоположную этому ускорению. Тогда все силы, действующие на каждую материальную точку, будут уравновешиваться (так, в разобранном примере уравновешиваются три силы КР, КТ, КМ. Сила КМ как раз и есть «центробежная сила инерции»).
Центробежная сила против центростремительной силы
Центробежная сила (в переводе с латинского означает «бегство от центра») описывает тенденцию объекта, следующего по искривленной траектории, лететь наружу от центра кривой. Это не совсем сила; это происходит из-за инерции — тенденции объекта противостоять любым изменениям в состоянии покоя или движения. Центростремительная сила — это реальная сила, которая противодействует центробежной силе и предотвращает «вылет» объекта, удерживая его вместо этого с равномерной скоростью по круговой траектории.
Сравнительная таблица
| Центробежная сила | Центростремительная сила | |
|---|---|---|
| Смысл | Склонность объекта по изогнутой траектории улететь от центра кривизны. Можно описать как «отсутствие центростремительной силы». | Сила, которая удерживает объект, движущийся с равномерной скоростью по круговой траектории. |
| направление | По радиусу круга, от центра к объекту. | Вдоль радиуса круга, от объекта к центру. |
| пример | Грязь отлетает с шины; детей выгнали на карусель. | Спутник, вращающийся вокруг планеты |
| формула | Fc = mv2 / r | Fc = mv2 / r |
| Определяется | Chistiaan Hygens в 1659 году | Исаак Ньютон в 1684 году |
| Это настоящая сила? | Нет; Центробежная сила — это инерция движения. | Да; центростремительная сила удерживает объект от «вылетания». |
Силы и инерция
Центробежная сила не является «реальной» силой — наблюдается тенденция к вылету наружу, поскольку объекты, движущиеся по прямой линии, как правило, продолжают двигаться по прямой линии. Это называется инерцией, и это делает объекты устойчивыми к силе, которая заставляет их двигаться по кривой.
Центростремительная сила — это «настоящая» сила. Он притягивает объект к центру и не дает ему «вылететь». Источник центростремительной силы зависит от рассматриваемого объекта. Для спутников на орбите сила исходит от силы тяжести. Если объект вращается на веревке, центростремительная сила обеспечивается натяжением веревки, а для вращающегося объекта сила обеспечивается внутренним напряжением. Для автомобиля, движущегося по дуге, центростремительная сила возникает из-за трения между автомобильными шинами и дорогой.
Если объект вращается должным образом, центробежные и центростремительные силы будут равны, поэтому объект не будет двигаться к центру вращения или наружу от него. Это будет поддерживать постоянное расстояние от центра.
направление

Направление центростремительной силы и скорости
Центростремительная сила направлена внутрь, от объекта к центру вращения. Технически он направлен перпендикулярно скорости тела, к фиксированной точке мгновенного центра кривизны траектории.
Центробежная сила направлена наружу; в том же направлении, что и скорость объекта. Для кругового движения скорость в любой данный момент времени находится в касательной к дуге движения.
формула
Обе силы рассчитываются по одной формуле:

где c c — центростремительное ускорение, m — масса объекта, движущегося со скоростью v вдоль пути с радиусом кривизны r .
Примеры центробежных и центростремительных сил
Некоторыми распространенными примерами центробежной силы на работе являются летящая с шины грязь, и дети ощущают силу, толкающую их наружу, когда они вращаются на кольцевой развязке.
Основным примером центростремительной силы является вращение спутников вокруг планеты.

Американские горки, пример центростремительной силы в действии

Спутник, вращающийся вокруг планеты, применяя центростремительную силу.

Иллюстрация центростремительной силы (красный вектор обозначен FT, сила натяжения в канате). Когда канат перерезан, центростремительная сила (натяжение каната) больше не будет действовать на объект. Таким образом, он больше не будет удерживаться в этом круговом пути FT и будет лететь по касательной.
Приложения
Знание центробежных и центростремительных сил может быть применено ко многим повседневным проблемам. Например, он используется при проектировании дорог для предотвращения заноса и улучшения сцепления на поворотах и пандусах. Это также позволило для изобретения центрифуги, которая отделяет частицы, взвешенные в жидкости, вращая пробирки на высоких скоростях.
Центробежная сила против центростремительной силы
Центробежная сила (На латыни «убегающий из центра») описывает тенденцию объекта, следующего по кривой траектории, лететь наружу, прочь от центра кривой. На самом деле это не сила; он возника
Содержание:
- Сравнительная таблица
- Силы и инерция
- Направление
- Формула
- Примеры центробежной и центростремительной силы
- Приложения
Центробежная сила (На латыни «убегающий из центра») описывает тенденцию объекта, следующего по кривой траектории, лететь наружу, прочь от центра кривой. На самом деле это не сила; он возникает из-за инерции — тенденции объекта сопротивляться любому изменению его состояния покоя или движения. Центростремительная сила это настоящий сила, которая противодействует центробежной силе и не дает объекту «вылететь», заставляя его двигаться с постоянной скоростью по круговой траектории.
Сравнительная таблица
| Центробежная сила | Центростремительная сила | |
|---|---|---|
| Смысл | Тенденция объекта, следующего по кривой траектории, улетать от центра кривизны. Можно описать как «отсутствие центростремительной силы». | Сила, которая заставляет объект двигаться с постоянной скоростью по круговой траектории. |
| Направление | По радиусу круга от центра к объекту. | По радиусу круга от объекта к центру. |
| пример | Грязь слетает с покрышки; детей вытолкнули на карусели. | Спутник на орбите планеты |
| Формула | Fc = mv2 / r | Fc = mv2 / r |
| Определяется | Чистиан Гигенс в 1659 году | Исаак Ньютон в 1684 году |
| Это настоящая сила? | Нет; центробежная сила — это инерция движения. | Да; центростремительная сила удерживает объект от «вылета». |
Силы и инерция
Центробежная сила не является «реальной» силой — наблюдается тенденция к вылету наружу, поскольку объекты, движущиеся по прямой линии, имеют тенденцию продолжать движение по прямой линии. Это называется инерцией, и это делает объекты устойчивыми к силе, которая заставляет их двигаться по кривой.
Центростремительная сила — это «настоящая» сила. Он притягивает объект к центру и не дает ему «вылететь». Источник центростремительной силы зависит от рассматриваемого объекта. Для спутников на орбите сила исходит от силы тяжести. Если объект вращается на веревке, центростремительная сила обеспечивается натяжением веревки, а для вращающегося объекта сила создается внутренним напряжением. Для автомобиля, движущегося по дуге, центростремительная сила возникает из-за трения между шинами автомобиля и дорогой.
Если объект вращается правильно, центробежная и центростремительная силы будут равны, поэтому объект не будет перемещаться к центру вращения или от него. Он будет поддерживать постоянное расстояние от центра.
Направление
Направление центростремительной силы и скорости
Центростремительная сила направлена внутрь от объекта к центру вращения. Технически он направлен ортогонально скорости тела, к фиксированной точке мгновенного центра кривизны траектории.
Центробежная сила направлена наружу; в том же направлении, что и скорость объекта. Для кругового движения скорость в любой момент времени находится по касательной к дуге движения.
Формула
Обе силы рассчитываются по одной и той же формуле:
где аc центростремительное ускорение, м — масса объекта, движущегося со скоростью v по траектории с радиусом кривизны р.
Примеры центробежной и центростремительной силы
Некоторые распространенные примеры действия центробежной силы — это грязь, стекающая с шины, и дети, чувствуя силу, толкающую их наружу, во время вращения на круговой развязке.
Главный пример центростремительной силы — вращение спутников вокруг планеты.
Американские горки, пример центростремительной силы в действии
Спутник, вращающийся вокруг планеты за счет центростремительной силы.
Иллюстрация центростремительной силы (красный вектор, обозначенный FT, сила натяжения каната). Когда веревка перерезана, центростремительная сила (натяжение веревки) больше не действует на объект. Таким образом, FT больше не будет удерживать его на этом круговом пути и улетит по касательной.
Приложения
Знание центробежных и центростремительных сил можно применить для решения многих повседневных задач. Например, он используется при проектировании дорог, чтобы предотвратить занос и улучшить сцепление с дорогой на поворотах и съездах. Это также позволило изобрести центрифугу, которая отделяет взвешенные в жидкости частицы путем вращения пробирок на высоких скоростях.